Технические науки. Транспорт

К.т.н., доцент Славич В.П., Грачов Д.В.

Херсонський національний технічний університет, Україна

РОЗШИРЕНА ЗАДАЧА ПРО МАКСИМАЛЬНИЙ

ПОТІК ВАНТАЖУ ІЗ ДОДАТКОВИМИ ОБМЕЖЕННЯМИ

Розширена модель задачі про максимальний потік вантажу у матричній постановці містить накладання на умови двох додаткових обмежень: за вивозом продукту від груп постачальників вантажу та за пропускними здатностями сполучень, що з’єднують постачальників зі споживачами. Нехай задано n постачальників A₁, A₂, …, A_m, у яких зосереджено вантаж відповідно у кількостях a₁, a₂, …, a_m од., та m споживачів даного вантажу B₁, B₂, …, B_m, яким даний вантаж необхідний відповідно у кількостях b₁, b₂, …, b_m од.. Та нехай задано матрицю чисел (a_ij), які можуть приймати два значення – 0 чи 1, в залежності від того, можна чи ні перевозити продукт від i-го постачальника до j-го споживача. Позначимо через – план перевезень та введемо додаткові обмеження.

1) Припустимо, що всі постачальники вантажу розділені на певні групи та задані обмеження за вивезенням загальної кількості продукту з кожної групи:

,

де r – кількість груп постачальників (кількість заводів);

I_k – множина номерів пунктів відправлень, що належать до k-ої групи.

S_k – максимальна кількість продукту, що може бути вивезена з k-ої групи.

2) Припустимо, що існують обмеження за пропускними здатностями маршрутів руху транспортних засобів, що задані у вигляді наступної матриці коефіцієнтів: .

Тоді модель задачі буде мати наступний вигляд.

1) Цільова функція:

2) Система обмежень: якщо ; якщо ;

при фіксованому i, ; при фіксованому j, ;

; .

Умови задачі та подальший хід пошуку оптимального плану представляється у вигляді табл. 1.

Таблиця 1

Постачальники	Споживачі				Запаси	Обмеження за вивозом вантажу із групи
	B1	B2	…	Bm
A1	a11 d11	a12 d12	…	a1m d1m	a1	S1
…	…	…	…	…	…
			…
			…			S2
…	…	…	…	…	…
			…
…	…	…	…	…	…	…
			…			Sr
…	…	…	…	…	…
An	an1 dn1	an2 dn2	…	anm dnm	an
Потреби	b1	b2	…	bm

Пропонується використання наступного модифікованого алгоритму.

1. Будуємо опорний план: .

2. Для кожного стовпця перевіряємо умову: .

3. Перевіряємо для рядка i₀ умову вивезення всього вантажу з i₀-го пункту.

1) Якщо виконується один з двох виразів: або , тоді закриваємо рядок i₀, а при виконанні умови закриваємо всі рядки k-ої групи, а клітинки даного рядка (рядків), для яких виконується умова і які розташовані у закритих стовпцях позначаємо знаком „–”, а відповідні їм стовпці розкриваємо. Клітинка (i₀j₀) позначається знаком „+”.

2) В разі виконання системи нерівностей: будуємо ланцюг клітинок.

4. Для перевезень в клітинках із „–” („+”) віднімаємо (додаємо) величину :

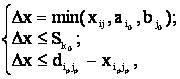
де – перевезення, що розташовані у клітинках ланцюга зі знаком „–”;

– номер групи постачальників, до якої належить рядок i₀.

При виконанні даного алгоритму при кожній побудові ланцюга клітинок кількість вантажу, що перевозиться, збільшується, тому після скінченої кількості повторень даної процедури буде отримано оптимальний план задачі.

Література:

1. Воркут А.И. Грузовые автомобильные перевозки. – Київ: Вища школа, 1986. – 447 с.

2. Славич В.П. Гібридна модель задачі про максимальний потік вантажу у матричній постановці із додатковими обмеженнями / В.П. Славич // Проблеми інформаційних технологій. – 2012. - №02(012). – С. 100 – 103.

3. Справочник по організации и планированию автомобильних перевозок /Под ред. И.Г.Крамаренко – Київ: Техніка, 1991. – 208 с.

4. Триус Е.Б. Задачи математического программирования транспортного типа. – М.: Советское радио, 1967. – 208 с.