Квасова Н.В., Васильев Е.М.
Воронежский государственный технический университет,
Россия
Математическая модель конкурентного
взаимодействия
элементов экономической системы
Рассмотрим замкнутую экономическую
систему, отраслевые элементы i (![]() ) которой
осуществляют свою производственную деятельность в условиях конкурентного
привлечения инвестиционных вложений ui(t). Общий объём
u(t) инвестиций
на рассматриваемом интервале времени t ограничен:
) которой
осуществляют свою производственную деятельность в условиях конкурентного
привлечения инвестиционных вложений ui(t). Общий объём
u(t) инвестиций
на рассматриваемом интервале времени t ограничен: 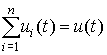 . Кроме того, будем учитывать, что валовой объём xi(t) производства
каждой отрасли удовлетворяет условию межотраслевого баланса [1-2]:
. Кроме того, будем учитывать, что валовой объём xi(t) производства
каждой отрасли удовлетворяет условию межотраслевого баланса [1-2]:
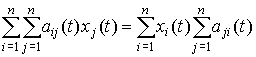 , (1)
, (1)
где aij(t) – элементы
технологической матрицы А; 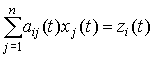 – производственное потребление;
– производственное потребление;
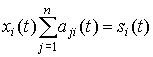 – затраты
промежуточной продукции; в общем случае
si(t)¹zi(t). Конечное
потребление продукции отраслей yi(t)=xi(t)-zi(t) не превосходит текущего спроса ymax,i(t), значение
которого может регулироваться механизмами институционального управления.
– затраты
промежуточной продукции; в общем случае
si(t)¹zi(t). Конечное
потребление продукции отраслей yi(t)=xi(t)-zi(t) не превосходит текущего спроса ymax,i(t), значение
которого может регулироваться механизмами институционального управления.
Для указанных общих условий функционирования
экономической системы построим динамическую модель изменения валовых выпусков xi(t) в виде:
![]() ,
(2)
,
(2)
где F
–нелинейный оператор. Возьмём начальное приближение к модели (2):
![]() , (3)
, (3)
в котором bi –коэффициент прироста валового
выпуска xi(t) за единицу времени; hi – коэффициент приростной
капиталоотдачи от внешних инвестиций ui(t).
Конкурентоспособность отрасли i в получении части ui(t) суммарных
инвестиций u(t) введём в (3) в виде коэффициента di(t) её инвестиционной
привлекательности, определив его как долю условно чистого продукта xi(t)-si(t) в отраслевых
затратах на производство: 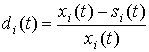 , тогда:
, тогда:
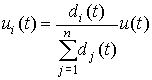 .
.
Если допустить возможность директивного
распределения части общего объёма инвестиций u(t), связанного,
например, с необходимостью устранения дисбаланса в развитии отраслей, то ui(t) можно
представить в виде:
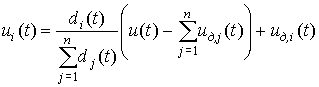 . (4)
. (4)
Поскольку коэффициент di(t) указывает
долю производственных затрат, содержащую амортизационные отчисления и затраты
на обновление основных фондов, то di(t) играет роль мультипликатора коэффициента bi прироста валового выпуска. С учётом (4) выражение (3) приобретает вид:
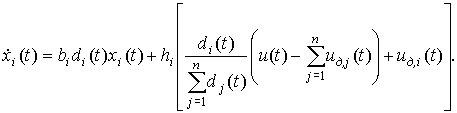 (5)
(5)
Влияние неравновесного состояния между
спросом ymax,i(t) и
предложением yi(t) конечного потребления (мультипликатор
неудовлетворённого спроса) введём в модель (5) в виде сомножителя 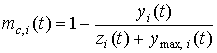 , учитывающего государственные закупки, входящие в ymax,i(t).
, учитывающего государственные закупки, входящие в ymax,i(t).
Допуская в пределе состояние отрасли,
близкое к полному удовлетворению конечного потребления yi, следует вместе с мультипликатором спроса mc,i(t) учесть
ограничение вида: 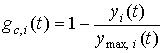 . Введение мультипликатора mc и ограничителя gc спроса в (5) приводит к выражению:
. Введение мультипликатора mc и ограничителя gc спроса в (5) приводит к выражению:
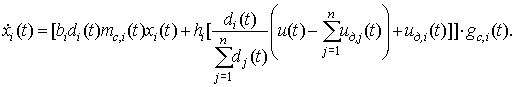 (6)
(6)
Рассмотрим теперь противоположную
ситуацию, когда хотя бы одна из взаимосвязанных отраслей с валовым выпуском xi(t), не
обеспечивающим рост производственного спроса zi(t), начинает
сокращать yi(t) до некоторого минимального уровня ymin,i(t) обязательных
поставок. При наступлении равенства: ![]() , рост производства всех отраслей j¹i региона начинает определяться
только темпом роста xi(t) отрасли i. Формализуем эту ситуацию введением в (6) ограничителя gп,i(t) в виде
множителя:
, рост производства всех отраслей j¹i региона начинает определяться
только темпом роста xi(t) отрасли i. Формализуем эту ситуацию введением в (6) ограничителя gп,i(t) в виде
множителя:
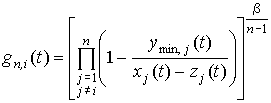 , (7)
, (7)
значение которого уменьшается при отставании темпов
роста валового выпуска xj(t) любой
отрасли j¹i от роста производственного потребления zj(t) на её продукцию;
b – показатель влияния ограничителя
gп,i(t).
Подставляя (7) в (6) получим модель развития
экономической системы:
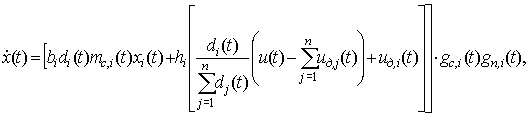 (8)
(8)
учитывающей конкурентное взаимодействие её элементов.
Литература:
1. Леонтьев В.В.
Экономическое эссе. Теории, исследования, факты и политика / В.В. Леонтьев. –
М.: Политиздат, 1990. – 415 с.
2. Тарасевич Л.С. Макроэкономика /Л.С. Тарасевич, П.И. Гребенников,
А.И. Леусский. – М.: Высшее образование, 2006. – 654 с.