Д.э.н. А.Г. Бутрин, В.А. Викулов

Южно-Уральский государственный университет, Россия

Применение теории массового обслуживания ДЛЯ оценкИ качества выполнения заказов потребителей в цепях поставок

Данная статья подготовлена в рамках госзадания Минобрнауки РФ 2012-2014 гг., проект "Организационно-экономическое обеспечение ресурсосберегающего инновационного управления предприятием".

Теория массового обслуживания – это раздел математики, изучающий системы, предназначенные для обслуживания массового потока заявок случайного характера. Все предприятия, интегрированные структуры, в т.ч. промышленные предприятия, интегрированные с поставщиками и потребителями функционируют как системы массового обслуживания.

Применение теории массового обслуживания предоставляет инструментарий для оценки вероятности риска возникновения ситуации отказа от выполнения заказа системным комплексом. Адаптируем терминологию, используемую в теории массового обслуживания к решению задачи в рамках концепции управления цепями поставок.

Системой массового обслуживания будем считать промышленное предприятия, интегрированное с поставщиками и потребителями, в который поступают заявки от конечных потребителей.

Промышленное предприятие, интегрированное с поставщиками и потребителями имеет в своем составе каналы обслуживания, в нашем случае это конкретные конфигурации цепи поставок. В концепции управления цепями поставок необходимо рассматривать простейший или пуассоновский поток заявок от конечных потребителей. Этому потоку присущи следующие признаки:

1. Стационарность – вероятность появления того или иного числа заявок на отрезке времени t зависит только от длины этого отрезка и не зависит от того, где именно располагается этот участок на оси времени;

2. Ординарность – в каждый момент времени в систему приходит только одна заявка;

3. Отсутствие последействия – все заявки приходят в систему независимо друг от друга.

Рассматриваемый поток называют «пуассоновским», так как количество заявок m, приходящееся на отрезок времени t, распределено по закону Пуассона:

где �� – плотность потока заявок, т.е. количество заявок в единицу времени.

На входе в систему массового обслуживания определяется плотность входного потока (количество заявок в единицу времени), на выходе из этой системы определяется плотность выходного потока μ, которая является величиной, обратной среднему времени обслуживания одной заявки. Плотность входного потока является величиной постоянной.

Внутреннее состояние систем – это вероятности того, что конкретная конфигурация цепи поставок неспособна выполнить своевременно заказ. Состояние промышленного предприятия, интегрированного с поставщиками и потребителями, с отказами описывается формулой Эрланга следующего вида:

,

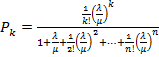где P_k –вероятности состояния системы (0≤k≤n), т.е.

P₀ – вероятность того, что все конфигурации цепи поставок способны выполнить своевременно заказ;

P₁ – вероятность того, что одна конфигурация цепи поставок неспособна выполнить своевременно заказ;

P_n – вероятность того, что все конфигурации цепи поставок неспособны выполнить своевременно заказ или вероятность отказа в обслуживании.

Рассмотрим применение инструментов теории массового обслуживания для решения задачи оценки вероятности возникновения риска отказа от выполнения заказа промышленным предприятием, интегрированным с поставщиками и потребителями на конкретном примере.

Имеется 3 альтернативных конфигурации цепи поставок для выполнения заказа. В месяце 25 рабочих дней. В месяц промышленное предприятие выполняет 50 заказов, среднее время выполнения заказа 1 день. Определим вероятность возникновения риска отказа от выполнения заказа.

В рассматриваемой задаче:

Система массового обслуживания – промышленное предприятие, интегрированное с поставщиками и потребителями.

Канал обслуживания – конкретная конфигурация цепи поставок.

Поток заявок - поток заказов от потребителей.

Обслуживание – выполнение заказа конкретной конфигурацией цепи поставок.

Поток заявок принимается простейшим (пуассоновским), тогда:

��==2 заказа в день (плотность входного потока),

μ==1 заказа в день (плотность выходного потока).

1. Определим вероятности того, что в течение 1 дня в промышленное предприятие, интегрированное с поставщиками и потребителями придут 0,1,2,3 и т.д. заявки.

Исходные данные: ��=2, t=1, m=0,1,2,3,4…

Результаты расчета по формуле Пуассона представлены в таблице 1.

Таблица 1

Кол-во заявок	0	1	2	3	4	5	6	7	8	9
Вероятности	0,137	0,274	0,274	0,183	0,091	0,037	0,012	0,003	0,001	0,0002

Как показывают данные таблицы наиболее вероятно получение одной или двух заявок в течении 1 дня, высока вероятность получения 3 и 4 заявок, а вероятность получения заявок 5 и более достаточно низка.

2. По формуле Элранга определим вероятности состояния системы, т.е. промышленного предприятия, интегрированного с поставщиками и потребителями. Результаты расчета представлены в таблице 2.

Таблица 2

Кол-во конфигураций цепи	0	1	2	3
Вероятности состояния системного комплекса	0,158	0,316	0,316	0,210

Как показывают данные таблицы 2 вероятность того, что все конфигурации цепи могут выполнить заказ (готовы к исполнению) является относительно низким – 15,8%, более высокую вероятность имеет неспособность выполнения заказа одной конфигурации цепи поставок 31,6%, вероятность неспособности выполнения заказа двумя конфигурациями цепи 31,6%. Вероятность возникновения ситуации отказа от выполнения заказа, т.е. ситуация неспособности всеми конфигурациями цепи выполнить заказ составляет 21,0%. Таким образом, можно сделать вывод, что вероятность возникновения риска отказа от выполения заказа промышленным предприятием, интегрированным с поставщиками и потребителями составляет 21,0%.

Список литературы:

1. Бутрин, А.Г. Проектирование и оптимизация бизнес-процессов интегрированных субъектов: монография / А.Г. Бутрин, В.И. Цаплин, Ю.В. Бутрина. – Челябинск: Издательский центр ЮУрГУ, 2011.– 240 c.

2. Бутрин, А.Г Методические основы управления цепями издержек интегрированных предприятий: учебное пособие/ А.Г. Бутрин. – Челябинск: Издательский центр ЮУрГУ, 2011.– 105 c.