К.т.н. П.В. Желтов, В.И Семенов, А.К. Шурбин
Чувашский государственный
университет, Россия
Кратномасштабный анализ сигналов с применением
непрерывного быстрого вейвлет-преобразования
Разделение (декомпозиция) сигналов на разнотипные
составляющие составляет основу кратномасштабного (многомасштабного) анализа
(КМА). Понятие «кратномасштабный анализ»
сформулировано 1986 году Малла и Мейером. Вейвлеты стали более
популярными после введения Малла концепции КМА для дискретных вейвлетов. Он же
первым применил вейвлеты для кодирования изображений. Популярность вейвлет-преобразования
(ВП) во многом объясняется тем, что оно успешно может использоваться для сжатия
изображений. Вейвлеты непосредственно связаны
с КМА сигналов. Идея КМА заключается в том, что
разложение сигнала производится по базису, образованному сдвигами и
кратномасштабными копиями вейвлетной функции. При выполнении КМА,
пространство сигналов L2(R) представляется в виде системы вложенных
подпространств ![]() . Разложение функций на вейвлетные ряды на заданном уровне
разрешения m, для дискретного ВП, выполняется по формуле [1,2]
. Разложение функций на вейвлетные ряды на заданном уровне
разрешения m, для дискретного ВП, выполняется по формуле [1,2]
![]() ,
,
где ![]() – скейлинг-функция или масштабирующая функция,
– скейлинг-функция или масштабирующая функция, ![]() – дискретный вейвлет. Значения коэффициентов
– дискретный вейвлет. Значения коэффициентов
![]() ,
,
![]() ,
,
на практике определяются с помощью
дискретного быстрого ВП (алгоритм Малла).
Скелинг-функцию и
вейвлет получают с помощью функциональных уравнений. Как правило, они не имеют
аналитического выражения.
Математические основы кратномасштабного анализа изложены во многих
источниках по дискретному ВП [1,2,3].
Авторами разработан алгоритм
обратного быстрого непрерывного ВП, который позволяет любой сигнал длительности
![]() , представить в виде
, представить в виде
![]() .
.
Используются
вейвлеты на основе производных функции Гаусса. А вычисления производятся в
частотной области с использованием быстрого преобразования Фурье, что позволяет
в реальном масштабе времени обрабатывать сигналы [4,5,6].
По аналогии
с дискретным ВП, все пространство сигналов L2(R) в целом, может быть представлено в
виде последовательности вложенных друг в друга замкнутых подпространств
соответствующих уровней m декомпозиции сигнала:
![]() .
.
"Размеры" подпространств непрерывно
расширяются по мере уменьшения значения m,
а объединение всех подпространств, в пределе дает пространство L2(R). Вейвлеты в подпространствах образуются путем масштабного
преобразования ![]() ,
,
![]() ,
,
где k –
целочисленные сдвиги.
Вейвлет в
подпространстве m
![]() .
.
Значение
параметра а равно 2.
Образуем из ![]() функции
функции ![]() такие, что (обозначение ‘‘ не означает двойного
дифференцирования)
такие, что (обозначение ‘‘ не означает двойного
дифференцирования)
![]() ,
,![]() и т.д.
и т.д.
Если сигнал
![]() принадлежит
пространству
принадлежит
пространству ![]() , то одновременно он входит и в пространство
, то одновременно он входит и в пространство ![]() и вместе с ним в этом
пространстве находится и сигнал
и вместе с ним в этом
пространстве находится и сигнал![]() . Уменьшение номера пространства позволяет изучать все более
и более мелкие детали и особенности сигнала с более высокочастотными
компонентами, т.е. переходить от грубого приближения к приближению более
высокого разрешения. Тогда сигнал с самым большим временным разрешением
. Уменьшение номера пространства позволяет изучать все более
и более мелкие детали и особенности сигнала с более высокочастотными
компонентами, т.е. переходить от грубого приближения к приближению более
высокого разрешения. Тогда сигнал с самым большим временным разрешением ![]() . Переменная m
называется, так же как для а,
масштабным коэффициентом, или уровнем анализа. Если значение m большое, то функция
. Переменная m
называется, так же как для а,
масштабным коэффициентом, или уровнем анализа. Если значение m большое, то функция ![]() есть грубая аппроксимация
есть грубая аппроксимация ![]() , в которой отсутствуют детали. При уменьшении значений m точность аппроксимации повышается.
, в которой отсутствуют детали. При уменьшении значений m точность аппроксимации повышается.
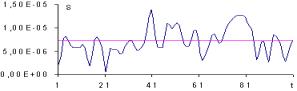
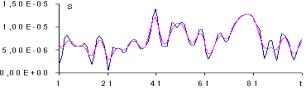
На рис. 1
представлены графики функции![]() и его различные аппроксимации, т.е. функции
и его различные аппроксимации, т.е. функции ![]() . Сигнал
. Сигнал ![]() разложен на 12 уровней декомпозиции. На рис. 1 представлена 1/20 часть сигнала. В
литературе по дискретному ВП, m-шаговое
дискретное ВП называется КМА. Максимальное значение m называется глубиной разложения (декомпозиции) сигнала. Для
разработанного алгоритма реконструкции глубина декомпозиции сигнала равна значению m + 1. На рис. 1 а) значение m
равно 11 – самая грубая аппроксимация сигнала. На всем протяжении сигнала
разложен на 12 уровней декомпозиции. На рис. 1 представлена 1/20 часть сигнала. В
литературе по дискретному ВП, m-шаговое
дискретное ВП называется КМА. Максимальное значение m называется глубиной разложения (декомпозиции) сигнала. Для
разработанного алгоритма реконструкции глубина декомпозиции сигнала равна значению m + 1. На рис. 1 а) значение m
равно 11 – самая грубая аппроксимация сигнала. На всем протяжении сигнала ![]() имеет почти постоянное значение.
имеет почти постоянное значение.
 а)
а)
 б)
б)
 в)
в)
 г)
г)
 д)
д)
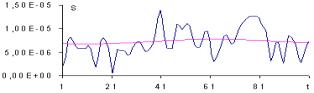
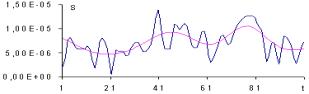
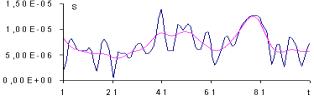
Рис. 1. Декомпозиция сигнала на разные уровни
На рис. 1 б) значение m
равно 6. На остальных графиках значение m
уменьшается от 3 до 1. Видно, что уменьшение масштабного коэффициента приводит
к более детальному описанию сигнала. Для
m = 0 коэффициент корреляции Пирсона
равен 0,999. Реконструированный сигнал точно повторяет контуры оригинала, и на
графике невозможно их отличить.
Сигнал так же можно исследовать в обратном порядке,
т.е. сначала представить мелкомасштабные составляющие, а потом добавлять к этим
составляющим более крупные детали, постепенно приближаясь к оригинальному
сигналу, как на рис.1, в обратном порядке.
Так же, как в случае с
одномерным сигналом, мы можем наблюдать двумерный сигнал на разных уровнях
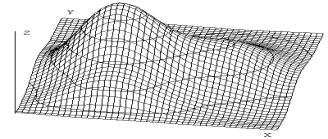
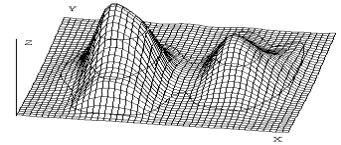
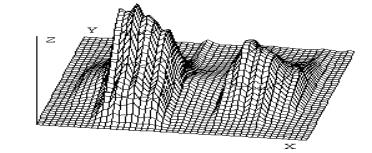
декомпозиции. На рис. 2 представлены графики двумерного объекта на
4-м, 1-м и 0-м уровнях декомпозиции.
 а)
а)
 б)
б)
 в)
в)
Рис. 2. Декомпозиция двумерного объекта
На графиках видно, что сигнал можно с
определенной точностью аппроксимировать в зависимости от ограничения количества
значений масштабирующего коэффициента m.
Тогда появляется возможность анализа функции или сигнала на различных уровнях
разрешения, или масштаба, также для фильтрации и сглаживания. Например, удалив
мелкомасштабные функции, мы можем выделить низкочастотный полезный сигнал или,
наоборот, удалив крупномасштабные функции выделить высокочастотный сигнал. Если
мы используем преобразование Фурье для
фильтрации сигнала, невозможно удалить локальные шумы, а ВП позволяет удалить и их.
В отличие от дискретного
ВП, данный алгоритм удобен и прост. Ненужно вычислять аппроксимирующие и
детализирующие коэффициенты для скейлинг- и вейвлет-функций. Нет необходимости
находить сплайновые и пакетные вейвлеты, койфлеты и делать всевозможные «трюки»
(по терминологии И. Добеши).
Литература:
1. Астафьева Н.М. Вейвлет-анализ: Основы теории и принципы применения. // УФН, т. 166, № 11, ноябрь, С.
1145 – 1170.
2. Новиков И.Я. Теория всплесков / И.Я. Новиков, В.Ю.
Протасов, М.А. Скопина. М.: Физматлит, 2005. 616 с.
3. Штарк Г.-Г. Применение вейвлетов для
ЦОС/ Г.-Г. Штарк. М.: Техносфера, 2007.
192 с.
4. Свидетельство об официальной
регистрации программ для ЭВМ №2007615024. Непрерывное быстрое
вейвлет-преобразование / Семенов В.И.; зарегистрировано в Реестре программ для
ЭВМ 4 декабря 2007 г.
5.
Свидетельство о государственной регистрации программы для ЭВМ №
2009616896. Непрерывное быстрое m + 1 шаговое вейвлет-преобразование /Семенов В.И.,
Желтов П.В.; зарегистрировано в Реестре программ для ЭВМ 11декабря 2009 г.
6. Свидетельство о государственной регистрации
программы для ЭВМ № 2010616103. Непрерывное сверхбыстрое вейвлет-преобразование
/ Семенов В.И..; зарегистрировано в Реестре программ для ЭВМ 16 сентября 2010 г.