ктн, доцент Василенко В. С., Дубчак О.В.

Національний авіаційний університет (НАУ), Україна

Цілісність інформаційних об’єктів і код умовних лишків

Інформаційні об’єкти, незалежно від форми їх початкового представлення, при зберіганні чи при передаванні у формі послідовності двійкових символів (нулів та одиниць) можуть розглядатися як деякі числа в тій чи іншій системі числення. Наприклад, певні сукупності таких двійкових символів можуть умовно розглядатися як символи в системі лишкових класів [1]. Порушення цілісності інформаційних об’єктів може розглядатися, в цьому випадку, як несанкціонована зміна величини початкового умовного числа. Для контролю цієї цілісності слід за певними правилами вводити ту чи іншу надлишковість. Тоді сукупність початкового умовного числа та введеної надлишковості може утворити певний завадостійкий код. При цьому можливості такого коду із виявлення порушень цілісності (спотворень початкового умовного числа) та їх усунення визначаються наявною надлишковістю. Як такий код можна розглядати код умовних лишків.

В цьому коді [1] групи розрядів початкового коду розглядаються як узагальнені символи – лишки від розподілу деякого умовного числа на сукупність – основ системи числення (і = 1, 2, …, п), де п = (т + k) – кількість таких лишків (груп розрядів), включаючи т узагальнених символів початкового коду та k надлишкових символів (в найпростішому випадку k = 1). У цьому випадку при (і = 1, 2, …, т), де – основа, за якою обчислюються надлишкові символи, за результатами декодування досить просто можна визначити факт наявності спотворень. З цією метою визначають, в який із інтервалів (піддіапазонів) величиною потрапляє спотворене число. Нагадаємо, що введення контрольної основи величиною р_n призводить до розширення діапазону представлення Р в р_n разів, іншими словами утворює р_n піддіапазонів величиною Р кожен.

Для визначення ж вимог до контрольної основи р_n слід здійснити певні дослідження. З цією метою нагадаємо, що спотворене число може бути представленим як сума початкового (не спотвореного) числа А та вектору спотворень Е: , де вектор спотворення Е в системі лишкових класів має лишки, що дорівнюють нулю, по усім основам, окрім тієї, де є спотворення. Тобто вектор спотворення є числом виду . При цьому величина спотворення визначається як , оскільки тільки числа, які діляться націло на мають у своєму представленні в СЛК такий набір лишків. В останніх виразах величина – контрольний (повний) діапазон представлення чисел в СЛК.

На числовій осі величина спотворення відображається точкою в деякому піддіапазоні “контрольного” діапазону [(Р + 1), R). Відповідно, процес спотворення початкового числа А відобразиться переміщенням точки А із робочого діапазону [0, P) в деякий піддіапазон із номером k. Звернемо увагу на те, що в піддіапазон із цим номером k спотворене число (А^/ = l_i×R_i + А₁ чи А^/ = l_i×R_i + А₂) може попасти (див. рис. 1) в залежності від величини початкового числа (А₁ чи А₂) та взаємного розташування лівих границь піддіапазонів – відповідно точок k×Р та l_i×R_i.

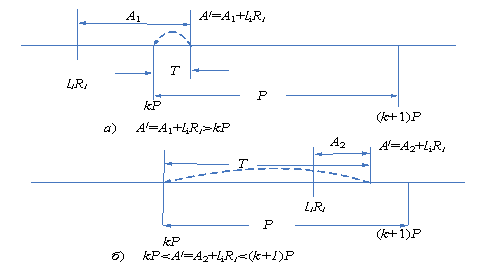
Рис. 1. Ілюстрація процесу нулізації

На рис. 1а зображена ситуація, коли величина початкового числа А₁ перевищує різницю між значеннями l_i×R_i та k·P, тобто коли А₁ > (k·P – l_i×R_i). Ця ситуація відповідає варіанту, коли визначена в наслідок нулізації величина Т є меншою ніж початкове, не спотворене число А.

Ситуація, зображена на рис. 1б відповідає варіанту, коли величина початкового числа А₂ є меншою ніж різниця між значеннями l_i×R_i та (k+1)·P. Отже визначена в наслідок нулізації величина Т є більшою ніж початкове, не спотворене число А.

В обох випадках результатом нулізації є число k·P, тобто ліва границя піддіапазону із номером k, а величина спотворення (чи довжина вектору спотворення) Е відповідає умові:

(k–1)·P < Е = l_i×R_i < (k+1)·P. (1)

Звернемо увагу на те, що один і той же результат нулізації може бути одержаним залежно від величини початкового (неспотвореного) числа А при попаданні вектора спотворення Е в межі діапазону, ширину якого можна визначити із виразу (1), якщо від лівої частини цього нерівняння відняти праву:

ΔЕ = (k+1)·P – (k–1)·P = 2P.

Отже результат декодування, який надасть можливість правильного визначення місця та величини спотворення, можна одержати лише у випадку, коли на числовій вісі можливі спотворення є рознесеними на величину, яка є не меншою ніж ΔЕ = 2P. Оскільки кількість піддіапазонів P в межах контрольного діапазону R = P·p_п визначається величиною контрольної основи (точніше, дорівнює) p_п, то і відстань між кінцями вектору спотворень залежить від величини p_п. Цей висновок повинен бути врахованим при визначення величини контрольної основи p_п. Неважко показати, що у цьому випадку слід вибирати значення контрольної основи p_п таке, що , де – найбільші із основ, що забезпечують робочий діапазон.