Арендаренко Л.С.

Евразийский национальный университет им. Л.Н.Гумилева, Астана, Казахстан

Ограниченность одного класса интегральных операторов в весовых пространствах Лебега

Доклад посвящен вопросу ограниченности в весовых пространствах Лебега интегрального оператора

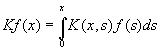(1)

с неотрицательным, непрерывным по совокупности переменных, ядром .

Обозначим через интервал . Пусть , , а и - неотрицательные функции, такие, что функции , , и локально интегрируемы на интервале .

Пусть ядро определено и измеримо на множестве . Рассмотрим интегральный оператор вида (1) с ядром удовлетворяющим следующему условию: найдутся неотрицательные измеримые функции и постоянная не зависящая от переменных, такие, что при любых выполнены неравенства

.

Тогда для оператора (1) справедлива следующая теорема.

Теорема 1. Пусть . Оператор (1) -ограничен тогда и только тогда, когда конечны величины

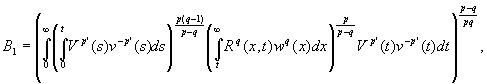
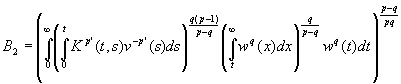
и при этом где - -норма оператора (1).

Для интегрального оператора, действующего по правилу

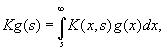(2)

с непрерывным неотрицательным ядром удовлетворяющим описанному выше условию, имеет место следующий результат.

Теорема 2. Пусть . Оператор (2) -ограничен тогда и только тогда, когда конечны величины

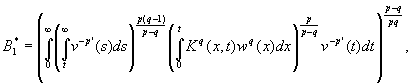
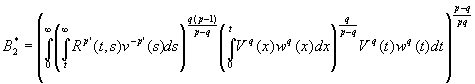
и при этом где - -норма оператора (2).

Поскольку в случае, когда параметры интегрирования удовлетворяют соотношению , любой -ограниченный оператор будет компактным, то полученные критерии ограниченности будут также и критериями компактности операторов (1) и (2).

Литература

1. Р. Ойнаров, Двухсторонние оценки нормы некоторых классов интегральных операторов // Тр. МИРАН. 1993, т.204, 240-250

2. Р. Ойнаров, Ограниченность и компактность интегральных операторов вольтерровского типа, Сибирский мат. журнал. 48(№5) (2007), 1100-1115