Модификация алгоритма  моделирования видеосигнала в измерительном сканирующем электронном микроскопе.

 

Докт. физ.-мат. наук Никитин А.В.

Институт искусств и информационных технологий. Московская область.

 

         В работе [1] сообщалось о создании пакета компьютерных программ для моделирования видеосигналов  в сканирующем электронном микроскопе (SEM), работающем в режиме прецизионных измерений размеров элементов интегральных схем с  нанометровыми проектными нормами.. Как там было показано, моделирование видеосигнала позволяет выявить, исследовать и, в конечном счете, - устранить ряд методических погрешностей, свойственных традиционным методам и алгоритмам измерений. Это имеет существенное значение для повышения достоверности результатов измерений, и основанных на таких измерениях решений о признании контролируемых изделий годными или заслуживающими списания в брак. Подробный анализ причин недостаточной достоверности измерительных результатов и негативных последствий таких  погрешностей  приведен в  работе  [2].

         Рассмотренные в [1] математические модели представляют собой набор  из двух пакетов: т.н. «точных» и «упрощенных» вариантов компьютерных программ.

В «точной» модели  по возможности учтены (почти) все особенности  и механизмы, влияющие на формирования видеосигнала в SEM: в т.ч. ускоряющее напряжение, диаметр пучка, сканирующего объект (разрешение),  условия его фокусировки, свойства объекта сканирования – материал контролируемого  «элемента» и окружающего его «поля», наличие рельефа, его характеристики,  механизмы проникновение первичных электронов вглубь объекта и их рассеяние на разных глубинах,  генерация вторичных электронов, их выход из объекта через рельефную поверхность,  повторные отражения от боковых стенок и донных частей  соседних рельефных образований и захват детектором.

Столь подробное описание привело к достаточно громоздким расчетным формулам, содержащим двойные интегралы (некоторые расчетные формулы приводятся в [1]). Несмотря на использование современных квадратур «быстрого» интегрирования по Ромбергу [3], расчеты большого числа интегралов специального вида требовали значительных вычислительных ресурсов, так что вычисление видеосигнала в сотне точках (видеопрофиль объекта) требовало существенных затрат процессорного времени - от единиц до десятков минут -  что сопоставимо с производительностью  расчетов по альтернативному и весьма распространенном методу  Монте-Карло [4].

В упрощенной модели использованы несколько правдоподобных (нестрогих) аналитических соотношений, касающихся проникновения быстрых электронов в твердое тело, отражений вторичных электронов от стенок соседних рельефных деталей, т.н. «апертурных» ограничений потоков, покидающих углубления рельефных структур и др. За счет этих, не всегда вполне корректных упрощений удалось резко повысить скорость расчетов, хотя их достоверность пришлось время от времени проверять сопоставлением с «точными» моделями.

В настоящем сообщении мы излагаем результаты паллиативного решения, позволяющего использовать преимущества «точной» модели, но без чрезмерных затрат вычислительных ресурсов.

Идея такого решения проста, даже тривиальна. Заметим, что согласно [1] в каждой точке вычисления видеосигнала приходится многократно – (до  3-х тысяч раз) – рассчитывать величину интеграла специального вида с весьма сложным подинтегральным выражением.   Часть потока, формирующая видеосигнал,  Р - определяется формулой:

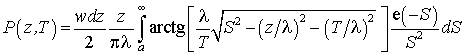        (3)     

где wdz – сила элементарного источника вторичных электронов (ВЭ), расположенного на глубине z;  λ – длина поглощения ВЭ в материале объекта; ;   Z– глубина залегания элементарного источника от поверхности; S – переменная интегрирования.

Анализ  формы этого наиболее важного интеграла, вычисляемого многократно,  показал, что его значение определяется только двумя параметрами: Z и T.  Именно для интегралов подобного типа с наибольшей выгодой можно использовать прием, описываемый ниже.

Итак, в предлагаемом способе мы используем двумерный массив интегралов ,  вычисленный заранее и сохраненный в памяти компьютера. Этот массив, создан по принципу «частой сетки», с разбивкой на 100 значений по  Z и T.  Разбивка по этим параметрам выбрана неравномерной: шаг разбивки выбран обратно пропорциональным производной по каждому параметру. Этим обеспечивался необходимый диапазон изменений  Z и Т:  от 0.01 до 90 нанометров, что перекрывает актуальные для моделирования значения этих параметров.  Этот двумерный массив используется для нахождения интегралов с заданными (требующимися, актуальными) значениями параметров Za и  Та

Для вычисления интегралов с промежуточными значениями параметров Zа и Tа (не совпадающими с узлами разбивки,) -  широко использованы приемы интерполяции –линейной и нелинейной. Опробование линейной и нелинейной (параболической) интерполяции оказалось неприемлемым из-за недостаточной точности интерполяционных процедур. Ниже описываются варианты использования многочленов третьей степени для этих целей.

Практический алгоритм поиска решений, реализован на компьютере и включает в себя следующие действия:

·        ввод актуальных значений параметров Zа и Tа   

·        фиксация значения одного из них, скажем, Zа 

·        проведение последовательного перебора табличных Тт и отыскание такого табличного ТТ, которое впервые превышает заданное значение Та.  Присвоение ему символа Т3. Присвоение соседним Т Т статусов табличных значений - Т1, Т2 и Т4

 

·       фиксация значения параметра Т1

·        последовательный перебор табличных Zт и нахождение такого его значения, которое впервые превышает заданное актуальное значение Zа. Присвоение ему символа Z3. Присвоение соседним табличным  значениям аргументов Zт символов  Z1, Z2 и Z4. Формируем таблицу  (4х4),  содержащую все комбинации символов Тi и Zi  в окрестностях точки с актуальными координатами: Та и Za

     Теперь формируем матрицу (4х4) табличных значений интегралов для окрестностей этой же точки:

 

 


I(Z1,T1)

I(Z1,T2)

I(Z1,T3)

I(Z1,T4)

I(Z2,T1)

I(Z2,T2)

I(Z2,T3)

I(Z2,T4)

I(Z3,T1)

I(Z3,T2)

I(Z3,T3)

I(Z3,T4)

I(Z 4,Т1)

I(Z 4,T2)

I(Z 4,T3)

I(Z 4,T4)

 

 

                  

                

 

 

 

Далее из матрицы выбираем первую строку табличных  значений  интегралов и аппроксимируем ее многочленом 3-й степени:
                                  I(Ti)Z=Z1= A·(Ti )3  + B·(Ti)2 +C·(Ti) +D.

Поскольку при постоянном Z=Z1 нам известны 4 разных интеграла  при разных Ti, то имеются 4 уравнения с 4-мя неизвестными: коэффициентами А, B, C, D. Решение такой системы серьезных трудностей не представляет. Таким образом, мы получаем аналитическую формулу, аппроксимирующую изменение значения интеграла вдоль верхней строки матрицы. Подставляя  эту формулу нужное (заданное, актуальное) значение Та, получаем решение, т.е. интеграл, соответствующий параметрам: Z=Z1 и T= Та.

         Теперь проделаем подобные процедуры со второй строкой матрицы. Получим аппроксимационную формулу для второй строки и значение интеграла с параметрами: Z=Z2 и T= Та.  

         Далее проделаем подобные процедуры с третьей строкой матрицы. Получим аппроксимационную формулу для третьей строки и значение интеграла с параметрами: Z=Z3 и T= Та.  

 Наконец, проделаем подобные процедуры с четвертой строкой матрицы. Получим аппроксимационную формулу для четвертой строки и значение интеграла с параметрами: Z=Z4 и T= Та.  

По полученным ранее значениям четырех интегралов с равными и точно заданными (!) параметрами Та проведем аппроксимационные процедуры для различных Zi. В полученную таким же образом аналитическую формулу, введем актуальное значение Zа  и получим окончательное значение интеграла с параметрами  Та и Zа. Таков используемый алгоритм вычислений. Компьютерная программа, реализующая этот алгоритм, составлена, отлажена и испытана.

Результаты опробования программы.

Испытания проводились путем сравнения интегралов, определенных по описанному методу (на основе 2-мерного массива)  c результатами прямого счета интегралов, вычисленными по алгоритму Ромберга  при начальной разбивке интервала интегрирования на 106 частей.

 При попадании Та и Za на узлы сетки разбиения  (т.е. при  отсутствии аппроксимационных процедур) – результаты прямого счета  и с 2-мерным массивом  совпадают до 11-го знака мантиссы.

Для интегралов с параметрами  Та и Za, находящихся между узлами сетки (в общих положениях) – расхождения  наблюдаются, но они составляют в худшем случае  несколько единиц в восьмом знаке мантиссы

 Подобный уровень погрешностей  был признан приемлемым для практических расчетов видеосигнала при его моделировании.

Время для расчетов серии (1 тысячи) различных интегралов  по методу частой сетки составило около 2.5 сек, а при прямом счете на вычисление одного интеграла затрачивалось около 55 секунд. Выигрыш по времени составил  не менее 20 000 раз.   

Таковы основные характеристики описанного приема вычислений интегралов специального типа  и, значит, возможностей моделирования с использованием рекомендуемой процедуры. Это открывает, в частности,  возможности моделирования видеосигналов по ходу проведения основной операции - измерения размеров – или использования результатов моделирования для коррекций измерительных результатов в процессе проведения самих измерений – практически  «в реальном времени» проведения измерительных процедур.

Это достижение стимулирует также разработки нового поколения методов измерений, включающих моделирование  в качестве  составной части собственно измерительных процедур.

 

 

Литература.

 

1.  Никитин А.В. «Использование математического  моделирования для измерений нано - размеров в микроэлектронике». «Измерительная техника», Вып. 12,  2011г. сс.25-29.

2. Никитин А.В. «Проблемы измерений размеров в микроэлектронной технологии»  

    http//www. NanoNewsNet.ru. 2010  Публикация  от 22 июля. 2010 г.

3.  Н. С. Бахвалов, Н. П. Жидков, Г. М. Кобельков  Численные методы. Бином, 2011, 640 с.  

4. S. Babin, S. Borisov, A. Ivanchikov,” Monte-Carlo modeling of SEM using CHARIOT software and opportunity for calibration of linewidth metrology”, Scanning,  V.29 No.2, p.80, 2007.