Математика/5.Математическое моделирование

 

 

Докт.физ.-мат.н.,проф. Валишин А.А.,асп.Степанова Т.С., докт.физ.- мат.н.,проф. Карташов Э.М.

Московский государственный университет тонких химических технологий им. М.В.Ломоносова (МИТХТ). Россия

 

Прогнозирование прочности полимерных и композиционных материалов в переменных температурно- силовых внешних условиях.  2.  Решение прямой задачи прогнозирования.

 

        Мы рассматриваем полимерные и композиционные материалы, для которых в температурном  диапазоне эксплуатации выражена температурно- временная зависимость прочности (ТВЗП). Прямая задача прогнозирования прочности состоит в определении прочности и долговечности при переменном температурно-силовом режиме испытания по известным параметрам статической температурно-временной зависимости прочности (ТВЗП). Эта задача решается с помощью обобщённого принципа суперпозиции внутренних повреждений. В простейшем случае для феноменологической меры накопления внутренних повреждений и  произвольного температурно- силового режима испытания  или эксплуатации критерий динамического разрушения  имеет вид:  

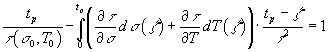                                        (1)

 

где - статическая долговечность при постоянных напряжении и температуре Т, tр – динамическая  долговечность в интересуцющем нас переменном температурно- силовом режиме. Рассмотрим несколько примеров решения прямой задачи.

        Моделирование испытаний на разрывной машине.

            Наиболее распространённый режим лабораторных испытаний на прочность - это испытания на разрывной машине с постоянной скоростью увеличения напряжения или с постоянной скоростью растяжения (постоянная скорость раздвижения зажимов разрывной машины) при постоянной внешней температуре. Для упругих тел эти два режима эквивалентны. В этом случае внешнее напряжение изменяется по закону

                                                                                            (2)

где - начальное напряжение,   - скорость изменения напряжения. Критерий динамического разрушения (1) принимает вид

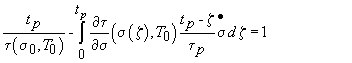                                         (3)       

Здесь - статическая долговечность в начальном состоянии. При решении прямой задачи прогнозирования считается известной статическая модель температурно - временной зависимости прочности (ТВЗП). К настоящему времени экспериментально установлены четыре эмпирические модели ТВЗП: Журкова, Регеля-Ратнера, Бартенева и Ратнера. Предположим, например, что для исследуемого материала справедлива модель Регеля-Ратнера статической ТВЗП, выражаемая формулой

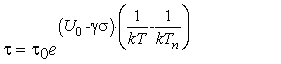                                                                 (4)

В эту формулу входят эмпирические константы . В нашу задачу здесь не входит обсуждение их физического смысла, скажем лишь, что они характеризуют свойства статической температурно – временной зависимости прочности (ТВЗП) материала. Подставляя формулу (4)  в (3)  и выполняя интегрирование, получим, что динамическая долговечность tp и разрывное напряжение  в рассматриваемом режиме испытания равны

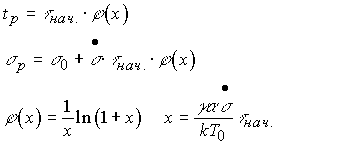                                                (5)

где

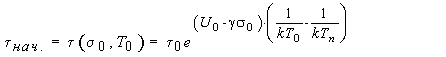 ,             (6)

статическая долговечность в начальном состоянии   Поскольку физические параметры статической ТВЗП -  в прямой задаче считаются известными, то по формулам (5),(6) можно предсказать прочность и долговечность при различных скоростях испытания , не выполняя эксперимента. В частности, видно, что при увеличении скорости нагружения  динамическая долговечность уменьшается. Полученные результаты позволяют предсказать прочность и в противоположном режиме испытания – режиме разгрузки, когда скорость изменения напряжения , что соответствует уменьшению напряжения. Видно, что в этом случае динамическая долговечность tp больше начальной статической долговечности и  с увеличением скорости разгрузки возрастает.

. Линейное температурное нагружение.

     Рассмотрим теперь температурное нагружение, когда напряжение σ остается в процессе испытания постоянным, а меняется только температура. Критерий разрушения в этом случае принимает вид:

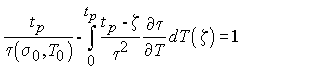                                         (7)

Примем для разнообразия статическую ТВЗП в виде модели Журкова 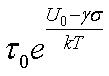                                                                                                                                                                                                          (8)                                          

Подставив это в (7) , получим

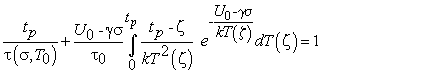                                   (9)

Это уравнение в дальнейшем и будем использовать для нахождения долговечности при переменной температуре испытания..

            Рассмотрим теперь случай, когда при постоянном напряжении σ температурный режим линейно изменяется во времени:

                                                                  (10)

где Т0 – начальная температура образца, а w – скорость изменения температуры. Если w>0 – происходит нагревание образца, если w<0 – то охлаждение. Обратимся к уравнению (9)  и

подставим туда (10). Вычисляя интеграл, получим

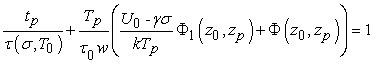                                             (11)

где обозначено

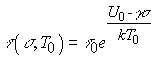                                                                                                            (12)

статическая долговечность при начальной температуре Т0; а

                                                                                             (13)

-температура образца в момент его разрушения, она может быть зафиксирована экспериментально;

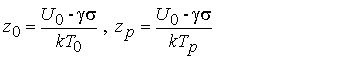                                        (14)

безразмерные параметры, а

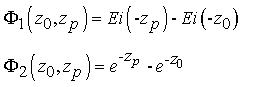                                                        (15)

 

безразмерные функции, и, наконец,

                                                  (16)

интегральная показательная функция.

Из уравнения (11)  легко получается теперь неизотермическая долговечность

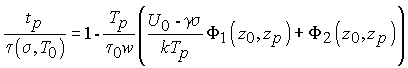                                (17)

Функции Φ1 и Φ2, определенные соотношениями (15)  зависят от скорости изменения температуры w через зависимость от нее параметра zP, определенного формулой (14).   В зависимости от знака w (нагревание или охлаждение), а также от ее величины, эти функции принимают значения разного знака. Соответственно и последнее слагаемое в формуле (17)  может менять знак. Это означает, что неизотермическая долговечность tP может быть как меньше, так и больше статической долговечности, соответствующей начальной температуре T0.

            Таким образом, если модель статической ТВЗП известна, то, решая прямую задачу прогнозирования, можно для каждого заданного режима испытания материала рассчитать параметры прочности в этом режиме. Этот процесс можно автоматизировать. Для этого созданный авторами электронный банк статических моделей ТВЗП нужно дополнить динамическими моделями для наиболее распространённых температурно – силовых режимов испытания. Тем самым, отпадает необходимость в проведении эксперимента.