СИНТЕЗ МАТРИЧНЫХ РЕГУЛЯТОРОВ ДЛЯ ПРОСТЫХ СИММЕТРИЧНЫХ СИСТЕМ РЕГУЛИРОВАНИЯ

А.Т. Уликян, А.А. Давтян

Рассмотрим -мерную линейную многомерную систему автоматического регулирования (МСАР) на рис. 1, где - передаточная матрица объекта регулирования размера , а - передаточная матрица регулятора того же размером.

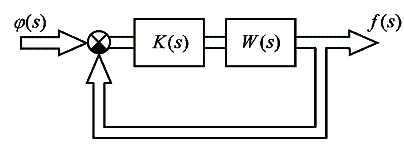
Рис. 1. Матричная структурная схема линейной МСАР

Допустим, передаточная матрица является простой симметричной, т.е. передаточные функции всех диагональных элементов одинаковы и, в дополнение, все передаточные функции недиагональных элементов также одинаковы [1, 2]. Если обозначить через диагональные элементы, а через все остальные элементы, то простая симметричная матрица может быть записана в следующем виде:

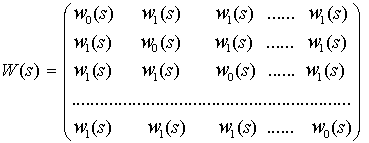(1)

Простые симметричные системы широко распространены в различных технических приложениях, связанных, например, с системами управления виброизоляционных платформ, системами гироскопической стабилизации, систем стабилизации вращением и т.д. [1]-[ 3].

Как известно [1,2], характеристические передаточные функции (ХПФ) простой симметоричной матрицы (1) при любом числе сепаратных каналов могут быть представлены в аналитической форме

(2)

и

. (3)

Иными словами, передаточная матрица простого симметричного объекта регулирования имеет при любом числе отдельных каналов только две различные одномерные характеристические системы. В теории многосвязного регулирования [1, 2] функции (2) часто называют передаточными функциями усредненного движения, а все остальные функции () (3) – относительного движения. Следует особо подчеркнуть, что все ХПФ (2), (3) простых симметричных объектов описываются обычными передаточными функциями с действительными коэффициентами [4].

В соответствии с рекомендациями, данными в [6], если многомерный объект регулирования описывается простой симметричной матрицей (1), то в качестве регулятора целесообразно использовать регулятор, передаточная матрица которого также является простой симметричной, т.е. имеет вид (1), где передаточные функции и следут заменить на и . ХПФ матрицы при этом будут иметь вид

(4)

и

, (5)

а ХПФ разомкнутой скорректированной системы запишутся в виде

. (6)

Отметим, что все ХПФ , и простой симметричной системы имеют вид (2)-(5), т.е. для каждой из матриц , и имеются только две различные ХПФ с действительными коэффциентами. Поэтому в данном случае достаточно легко определить передаточные функции и регулятора по найденным, на основании известных методов классической теории регулирования [4], "желаемым" ХПФ регулятора в (6). Действительно, из (4), (5), после несложных преобразований имеем следующие простые выражения:

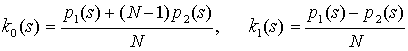. (7)

Таким образом, проектирование матричного регулятора для простой симметричной САР произвольной размерности фактически сводится к расчету двух обычных одномерных систем стандартными методами.

Пример. В последние годы в различных технических системах, таких как тестовые лабораторные установки, системы виброизоляции, системы управления вторичным зеркалом больших астрономических телескопов и т.д., большое применение получили так называемые гексаподы [5].

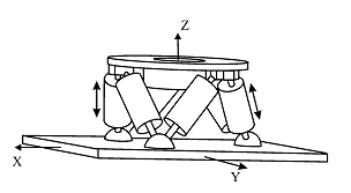
Рис. 2. Кинематическая схема гексапода

Конструктивно гексаподы представляют собой платформу с полезной нагрузкой, установленную на шести объединенных попарно стойках, каждая из которых может изменять длину при помощи специальных линейных приводов (рис. 2). В общем случае гексаподы обеспечивают шесть степеней свободы. Если же каждая пара стоек работает синхронно на уменьшение или увеличение длины, то гексаподы имеют три степени свободы. Ввиду конструктивной симметрии гексаподов, их системы управления описываются простыми симметричными матрицами размера , имеющими вид [5]:

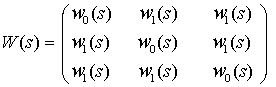. (8)

Выберем передаточные функции и в (8) в виде:

.

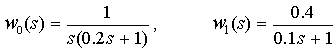ХПФ усредненного движения (2) при этом имеет вид:

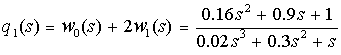, (9)

а все ХПФ относительного движения одинаковы и имеют, исходя из уравнений (3), вид:

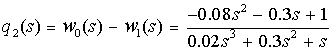. (10)

На рис. 3 показаны характеристические годографы ХПФ (9) и (10), откуда видно, что устойчивость рассматриваемой простой симметричной системы без коррекции определяется ХПФ относительного движения (10). Запасы устойчивости по амплитуде и фазе системы, определяемые по годографу , при этом равны: дб и .

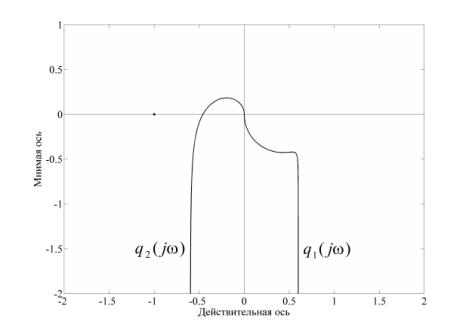
Рис. 3. Характеристические годографы гексопода без коррекции

Выберем теперь такой матричный регулятор, при котором ХПФ усредненного движения скорректированной системы останется без изменения, т.е. будет совпадать с ХПФ гексапода [что соответствует ], а коррекция ХПФ относительного движения будет определяться интегро-дифференциальной передаточной функцией

, (11)

имеющей полюс в -0.004 и нуль в -0.025. Передаточная функция (11) рассчитана на основе стандартных методов [4], исходя из условия повышения запасов устойчивости по амплитуде и фазе характеристических систем относительного движения до значений дб и .

Подставив и выражение для (11) в (7), получим

. (12)

Как видно из (12), требуемые взаимные связи компенсатора описываются реальным дифференцирующим звеном. Характеристические годографы скорректированной системы с передаточными функциями матричного регулятора и (12) показаны на рис. 4, где более тонкие линии соответствуют годографам и .

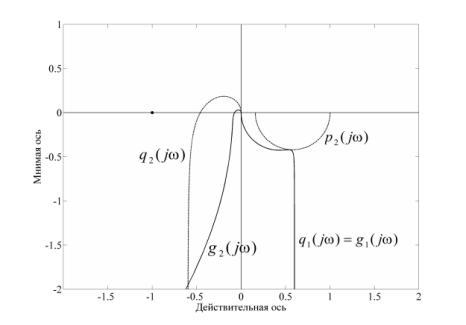
Рис. 4. Характеристические годографы скорректированной системы

ЛИТЕРАТУРА

1. Gasparyan O.N. Linear and Nonlinear Multivariable Feedback Control: A Classical Approach, John Wiley & Sons, UK, 2008, 356 P.

2. Гаспарян О.Н. Теория многосвязных систем автоматического регулирования, ГИУА, Ереван, Изд-во «Асогик», 2010, 380 с.

3. Хорол Д. М., Барский А. Г., Орлова М. С. Динамические системы с одноканальными измерителями.- М.: Машиностроение, 1976.

4. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования, М.: Наука, 2003, 560 с.

5. Joshi A. A., Kim W.-J. Modeling and Multivariable Control Design Methodology for Hexapod-Based Satellite Vibration Isolation, ASME Journal of Dynamic Systems, Measurement and Control, Vol. 127, No. 4, pp. 700–704, December 2005.

6. Гаспарян О.Н., Егиазарян Г.Г., Уликян А.Т. К выбору матричных регуляторов многомерных циркулянтных систем автоматического регулирования//Информационные Технологии и Управление, 2011, № 4.