В.Е. Билозёров, С.А. Волкова, Л.В. Подгорная

ГВУЗ «УГХТУ», каф. ВТ и ПМ

г. Днепропетровск, пр. Гагарина, 8

Построение конуса устойчивости для частных случаев квадратичных систем: вольтерровские модели

Ограничимся рассмотрением двумерных моделей. Без потери общности можно считать, что начало координат является стационарной точкой. В этом случае общий вид двумерной модели таков:

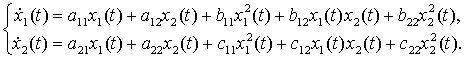
Исследование глобальной устойчивости вольтерровских систем

Анализ квадратичной системы общего вида неприменим непосредственно к вольтерровским системам. Предложим для систем такого вида другой метод анализа, основанный на использовании логарифмического преобразования координат.

Обозначим через Rⁿ вещественное линейное пространство вектор-столбцов размерности n (в дальнейшем мы будем называть его пространством состояний), а через x^T = (x₁, ..., x_n) – неизвестный вектор из Rⁿ (называемый в дальнейшем вектором состояний), координаты которого являются функциями времени t. Рассмотрим модель Лотки-Вольтерры в виде

, i=1,2,…,n .

Будем считать ее невырожденной, т.е. det A ¹ 0 (где A={a_ij}).

Теорема . Если для любой диагональной матрицы W с положительными диагональными элементами матрица DW – гурвицева, то для системы начало координат глобально асимптотически устойчиво.

Пример 1. Рассмотрим систему

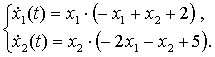(1)

Здесь d₁ = 7/3, d₂ = 1/3. Тогда

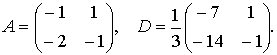
Легко проверить, что условия теоремы для системы выполнены. Поэтому точка (7/3,1/3)^T системы (1) глобально асимптотически устойчива в первом ортанте. Соответствующий фазовый портрет приведен на рис.1.

Рис. 1. Фазовый портрет глобально устойчивой в первом ортанте модели (1)

Пример 2. Примера рассмотрим систему

(2)

Для данного примера все условия теоремы выполнены. Следовательно, первый ортант является областью глобальной устойчивости независимо от параметров b₁, b₂ и b₃, что подтверждают и результаты численных расчетов (рис. 2).

Рис. 2. Фазовый портрет трехмерной модели (2), глобально устойчивой в первом ортанте