Математика/ 5. Математическое моделирование

Мурадилова Г.С.

Кокшетауский государственный университет им. Ш.Уалиханова, Казахстан

МОДЕЛЬ УПРАВЛЕНИЯ ПРОЦЕССОМ ОБУЧЕНИЯ

Одной из характерных особенностей современной эпохи является все возрастающее внимание к проблемам оптимального управления. Проблемы управления реальными процессами в механике, технологии, экологии, экономике и даже в образовании, приводят к сложным задачам оптимального управления. Целью данной работы является иллюстрация использования теории и методов оптимального управления в задаче по обучению студентов.

Рассмотрим задачу управления процессом обучения студентов. Математическая модель процесса обучения задается дифференциальным уравнением [1]:

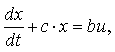
(1)

где x(t)- уровень знаний студента в момент времени t; x₀ - начальный уровень знаний; u(t) - интенсивность работы студента в момент времени t; 0tT; T- длительность семестра.

Управлением является функция u(t), которая удовлетворяет ограничениям

, (2)

где - верхний предел возможной интенсивной работы студента.

Рассмотрим задачу поиска наибольшего значения функционала

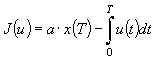, (3)

означающего достижение наибольшего уровня знаний студента к концу семестра.

В рассматриваемой задаче (1) - (3) коэффициенты a, b, c - положительные параметры, . Введем пространство управлений

.

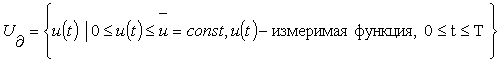Таким образом, возникает следующая задача оптимального управления:

Задача 1. Среди всех управлений найти такое, при котором для соответствующего решения уравнения (1) функционал (3) достигает максимального значения.

Для рассматриваемой задачи оптимального управления получены следующие результаты:

Теорема 1. Для любого управления уравнение (1) имеет единственное решение , удовлетворяющее неравенству:

,

где С₁ - некоторая константа, зависящая от параметров уравнения.

Теорема 2. Оптимальное управление в задаче (1) - (3) существует, т.е. существует измеримая функция , для которой .

Для вывода условий оптимальности в форме принципа максимума Понтрягина введем функцию , являющуюся решением вспомогательного уравнения

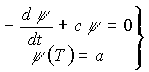(4)

Обозначим через .

Теорема 3. (принцип максимума Понтрягина)

Для того чтобы процесс , был оптимальным в задаче (1) - (3) необходимо и достаточно, чтобы существовала функция , являющаяся решением дифференциального уравнения (4) и чтобы почти для всех t из функция достигала максимума по u при

.

Литература:

1. Lee C.S., Leitmann G. On a Student-Related Optimal Control Problem.// Journal of optimization theory and applications: Vol.65, № 1, april 1990.

2. Мусабеков К.С., Мурадилова Г.С. Приложение математической теории оптимального управления в учебном процессе.// Функционально-дифференциальные уравнения и их приложения (материалы второй Международной конференции) - Махачкала, ДГУ, 2005 г.