А.И. Акмолдина

ОГРАНИЧЕННОСТЬ КОЭФФИЦИЕНТА ПРОНИЦАЕМОСТИ

Костанайский государственный университет им. А. Байтурсынова

This work about the limitation of factor of permeability is considered

Лемма 1. Если , то для решения задачи

(1)

(2)

имеют место оценки

,

.

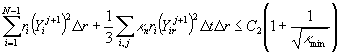Используя лемму 1 можно доказать ограниченность коэффициента

.

Если ограничена, сверху и снизу, строго отделено от нуля, тогда коэффициент также обладает аналогичными свойствами. Функция является кусочно-постоянной. Поэтому

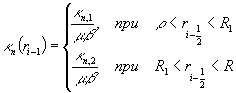
Обозначим . Значение определяется из условия минимизаций функционала

.

В таком случае имеет место равенство

.

.

Функцию определяем следующим образом

. (3)

Тогда

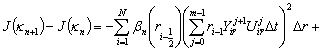
(4)

Чтобы доказать ограниченность , умножим (3) на и суммируем по от до . Тогда

.

Суммируем по от до произвольного

.

Левый часть знака равенства оценивается сверху по модулю:

.

Используем лемму 1, тогда

.

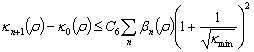Пусть .

В таком случае вытекает неравенство

.

Где достаточно малое число выбирается из условия

.

Из предпоследнего неравенства следует ограниченность функций . Аналогичным образом доказывается ограниченность функций .