З.Б.
Биртаева
КОНВЕКТИВНОЕ
РАСПРОСТРАНЕНИЕ ТЕПЛА.
Костанайский политехнический колледж
This work about convective
distribution of heat is described.
В области ![]() решается задача
решается задача
![]() (1.1)
(1.1)
![]() (1.2)
(1.2)
где ![]() и
и ![]() соответственно температуры и влажность грунта;
соответственно температуры и влажность грунта; ![]() - удельная масса,
- удельная масса, ![]() - теплоемкость,
- теплоемкость, ![]() - теплопроводность грунта. А также
- теплопроводность грунта. А также ![]() - коэффициент влагопроводности грунта,
- коэффициент влагопроводности грунта, ![]() - термоградиентный коэффициент.
- термоградиентный коэффициент.
Для уравнении (1.1) и (1.2) ставятся
следующие начально – граничные условия:
![]() (1.3)
(1.3)
![]() (1.4)
(1.4)
![]() (1.5)
(1.5)
![]() (1.6)
(1.6)
Кроме этого задаются температура и влага
грунта на поверхности земли:
![]() (1.7)
(1.7)
Требуется определить коэффициент
теплопроводности грунта ![]() .
.
Считаем, что система (1.1) – (1.6)
справедливо для любых последовательных значении ![]() и
и ![]() . Решение системы (1.1) – (1.6) при
. Решение системы (1.1) – (1.6) при ![]() обозначим через
обозначим через ![]() а при
а при ![]()
![]()
Тогда для разности
![]()
![]()
Система (1.1) – (1.6) записывается в
виде![]()
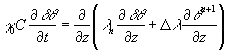 (1.8)
(1.8)
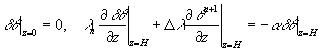 (1.9)
(1.9)
![]() (1.10)
(1.10)
![]() (1.11)
(1.11)
![]() (1.12)
(1.12)
Введем скалярные произведения
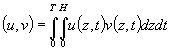
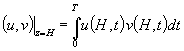
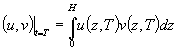
Умножим (1.8) на произвольную функцию ![]() и интегрируем по всем
внутренним точкам области
и интегрируем по всем
внутренним точкам области ![]() . Тогда
. Тогда
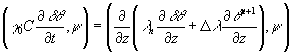
Интегрируя по частям получим
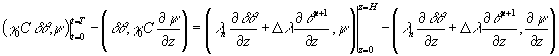 Учитывая граничные условия (1.9) и (1.10), кроме того полагая
Учитывая граничные условия (1.9) и (1.10), кроме того полагая
![]() выводим, что
выводим, что
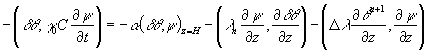
Еще раз интегрируя по частям, имеем
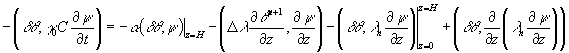 Или учитывая (1.9) перепишем его в виде
Или учитывая (1.9) перепишем его в виде
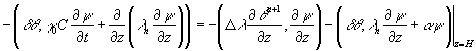 (1.13)
(1.13)
Умножим (1.11) на функцию ![]() и интегрируем по всем внутренним точкам области
и интегрируем по всем внутренним точкам области ![]() . Тогда
. Тогда
![]()
Интегрируем по частям по двум переменным
![]() и
и ![]() :
:
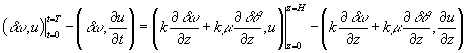
Положим, что
![]() и
и ![]() . Тогда используя начально-граничные условия (1.12) имеем
. Тогда используя начально-граничные условия (1.12) имеем
![]()
Или еще раз применяя формулу
интегрирование по частям получим
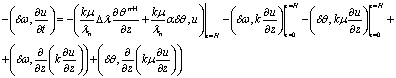
Учитывая граничные условия (1.3), (1.9)
и (1.12) получаем
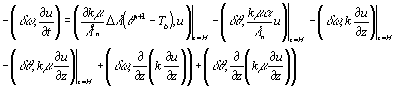 (1.14)
(1.14)
Складываем (1.13) и (1.14):
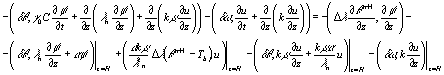 Функция
Функция ![]() и
и ![]() выбираются так, чтобы
имело место равенства
выбираются так, чтобы
имело место равенства
![]()
Тогда
![]()
Дополнительно ставятся следующие
граничные условия для ![]() и
и ![]() на поверхности земли:
на поверхности земли:
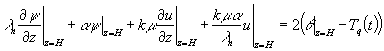
После этого получается неравенство
![]() (1.15)
(1.15)
В ходе вывода формулы (1.15) нами была
получена задача
![]() (1.16)
(1.16)
![]() (1.17)
(1.17)
![]() (1.18)
(1.18)
![]() (1.19)
(1.19)
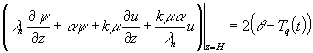 (1.20)
(1.20)