З.Б. Биртаева
КОНВЕКТИВНЫЙ ПЕРЕНОС В МНОГОСЛОЙНОМ
ГРУНТЕ.
Костанайский политехнический колледж
This work about convective
carrying over to a multilayered ground is described.
В области ![]() рассматривается
конвективное распространение тепла. Уравнение движение, движение влаги и тепла
записываются в следующем виде:
рассматривается
конвективное распространение тепла. Уравнение движение, движение влаги и тепла
записываются в следующем виде:
![]() (1)
(1)
![]() (2)
(2)
Для
уравнений (1) ставятся следующие начально-граничные условия
![]()
![]() (3)
(3)
![]() (4)
(4)
Уравнение
влаги (2) решается при следующих условиях
![]()
![]() (5)
(5)
Кроме
того, при переходе от одного слоя к другому слою ставятся условия
![]() (6)
(6)
![]() (7)
(7)
Здесь
![]() координаты точки
перехода.
координаты точки
перехода.
Для
того чтобы определить коэффициент теплопроводности задаются условия
![]()
![]() (8)
(8)
Коэффициент
теплопроводности определяется итерационным методом. Решение системы (1)-(7) при
значениях ![]() и
и ![]() обозначим через
обозначим через ![]() и
и ![]() соответственно. Тогда
для разности
соответственно. Тогда
для разности
![]()
выводится
система
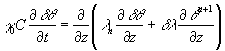 (9)
(9)
![]()
![]() (10)
(10)
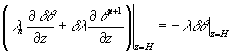 (11)
(11)
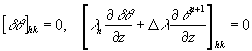 (12)
(12)
Здесь
![]() А для влаги
соответствующее уравнение записывается в виде
А для влаги
соответствующее уравнение записывается в виде
![]() (13)
(13)
![]()
![]() (14)
(14)
![]() (15)
(15)
В
данном случае предполагается, что ![]() . Данное предположение не нарушает общность постановки
задачи. Принимая во внимание начальные условия из (10) и дополнительно к этому
полагая,
. Данное предположение не нарушает общность постановки
задачи. Принимая во внимание начальные условия из (10) и дополнительно к этому
полагая, ![]() получаем равенство
получаем равенство
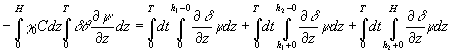
Предполагаем
непрерывность функции ![]() в точках
в точках![]()
То
есть ![]() или, иначе
или, иначе ![]()
Учитываем
непрерывность функций ![]() в точках
в точках ![]() , т.е.
, т.е. ![]() и принимая во внимание
граничное условие
и принимая во внимание
граничное условие ![]() выводим, что
выводим, что
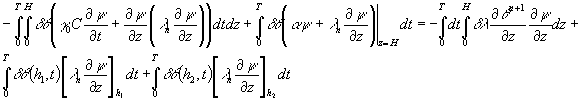 (16)
(16)
Для
функций ![]() ставим следующие конечные, граничные и внутренние граничные
условия
ставим следующие конечные, граничные и внутренние граничные
условия
![]()
Предполагаем
непрерывность величины ![]() в точках
в точках ![]() и
и ![]() , то есть
, то есть ![]()
Тогда
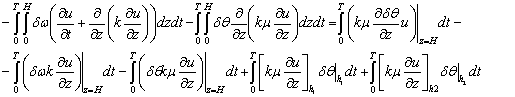 (17)
(17)
Складывая
(16) и группируя подобные слагаемые, получим
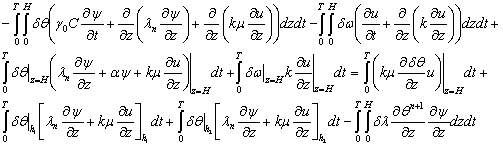
Предполагаем
выполнение следующих равенств
![]()
![]()
![]()
Тогда
![]() (18)
(18)
Учитывая
граничные условия преобразуем (11)
![]()
Подставляем
в (18), тогда
![]()
Тогда
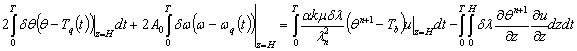 (19)
(19)
Получены
следующие сопряженные задачи
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
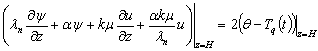 (25)
(25)
![]() (26)
(26)