З.Б. Биртаева

ПРИБЛИЖЕННЫЙ МЕТОД ДЛЯ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ТЕПЛОПРОВОДНОСТИ

This work about the approached method for definition of factor of heat conductivity is described.

Зададим начальное приближение , а следующее приближение определяется из монотонности функционала

где заданные значения температуры и влаги на поверхности земли.

Рассмотрим последовательные значения коэффициента теплопроводности и Ясно, что решение системы при обозначим через , а при обозначим через

Разность этих величин обозначим через

В целях упрощения записи иногда будем применять обозначения

или

Тогда для разности и получается разностная задача

(1)

(2)

(3)

(4)

Для краткости изложения в дальнейшем используются обозначения

Умножим (1) на произвольную функцию и суммируем по всем внутренним точкам области . Тогда

Левая часть знака равенства суммируем по частям, по переменной , а правая часть по переменной

Предполагаем, что

Тогда учитывая начально – граничные условия (2), выводим

Вторую сумму в правой части знака равенства суммируем по частям по переменной .Тогда

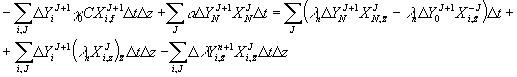
Собирая подобные величины в левую часть знака равенства, получим

(4)

Положим, что

Тогда, учитывая условие, имеем равенство

Учитывая однородные условия

и перегруппируя слагаемые, записываем предпоследнее равенство в виде

Полученное равенство складываем с равенством (4). Тогда

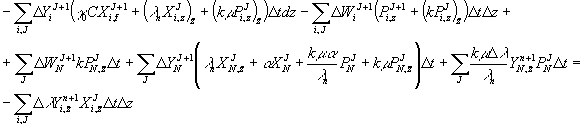Предполагаем, что для функции и имеют место равенства

Тогда

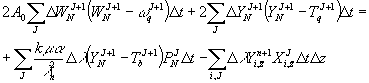(5)

Собирая поставленные условия для функции и , получаем задачу

(6)

(7)

(8)

(9)

(10)