МЕТОДЫ АППРОКСИМАЦИИ ОБОБЩЕННЫХ ФУНКЦИЙ

И ИХ ПРОИЗВОДНЫХ

Обобщенные функции получили широкое распространение в XX веке, когда новые задачи в физике и математике привели к настоятельной потребности расширить определение функции. Например, при решении задач квантовой механики обычного определения функции, при котором каждому значению аргумента , взятому из некоторой области, по определенному правилу ставится в соответствие одно значение , оказалось недостаточно. Физики использовали функции, которые нельзя было определить с точки зрения обычной теории функций.

Пусть ─ линейное пространство, элементами которого являются функции в смысле обычного определения.

Если имеется правило, по которому каждой функции ставится в соответствие некоторое число, то говорят, что на множестве задан функционал. Обозначим функционал , или проще .

Функционал называется линейным, если выполняется условие .

Функционал называется непрерывным, если из условия следует выполнение условия , .

Будем рассматривать функции на множестве .

Назовем функцию финитной, если она вне конечного промежутка обращается в ноль, причем границы промежутка зависят от . Всякую непрерывную финитную функцию назовем основной. Совокупность основных функций обозначим .

Пусть функция является обычной в смысле определения, причем она является непрерывной за исключением, быть может, конечного числа точек разрыва, и ограниченной на любом конечном промежутке.

Определим функционал интегралом 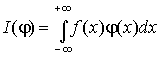, который для любой основной функции будет конечным. Функционал такого вида называется регулярным функционалом.

Определение. Обобщенной функцией называется любой линейный непрерывный функционал , заданный на множестве , обладающий свойствами

1. ;

2. , если в .

Не всякая обобщенная функция является регулярной Обобщенная функция, которая не может быть представлена интегралом 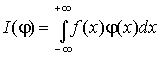, называется сингулярной. Примером сингулярной обобщенной функции может служить функция . Эту функцию называют - функцией или функцией Дирака.

В этой статье предложены методы, с помощью которых можно аппроксимировать сингулярные обобщенные функции и их производные, например, - функцию.

Смысл сингулярных обобщенных функций можно понять, основываясь на их приближениях, воспринимая обобщенную функцию как предел некоторой аппроксимирующей последовательности обычных функций. Например, ─ функцию можно рассматривать как предел последовательности ступенчатых функций. Однако использование последовательности ступенчатых функций не позволяет в должной мере осуществить представление производных ─ функции, которые, в свою очередь, также являются обобщенными функциями. Проблема заключается в том, что ступенчатые функции имеют точки разрывов, в которых они не являются дифференцируемыми. Поэтому для представления производных ─ функции нужно воспользоваться аппроксимирующей последовательностью аналитических функций, имеющих производные любого порядка.

Выражение, используемое для аппроксимации в этом случае, может иметь вид рекурсивной последовательности функций , где В частности, на рис. 1 изображен график функции

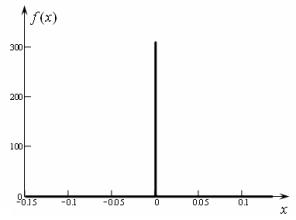
Рис. 1. График приближения - функции

Как видно из графика, предложенные методы аппроксимации дают гораздо достаточно точное приближение - функции. Причем, точность аппроксимации можно повысить до сколь угодно большой степени, увеличивая число вложенных функций. Высоту пика аппроксимации (амплитуду) можно определить по интегральному условию в определении - функции.

Для определения высоты пика аппроксимации воспользуемся тем фактом, что ─ функция является производной функции Хевисайда или функции единичного скачка, которая определяется так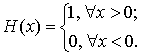

Функцию Хевисайда можно аппроксимировать последовательностью функций вида , где последовательность функций определяется соотношением

и рассматривается на отрезке . Например, на рис. 2 показаны графики трех последовательных приближений

,

,

,

где .

Толщина графика увеличивается по мере увеличения номера аппроксимирующей зависимости.

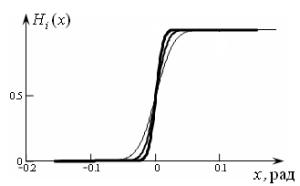
Рис. 2. Графики аппроксимаций функции Хевисайда

Находя первые производные приближений функции Хевисайда, мы получим последовательные приближения ,  и для ─ функции. Их графики изображены на рис. 3.

Дифференцируя аппроксимирующие функции рассмотренной последовательности , получим

.

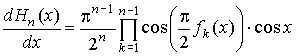Подставляя в полученное выражение для производных , с учетом четности ─ функции, найдем значение для высоты пика аппроксимирующих функций

.

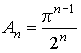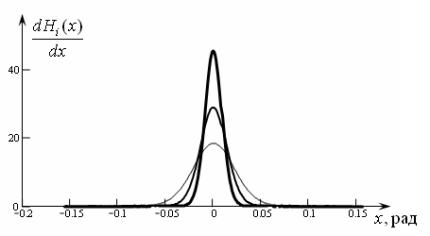
Рис. 3. Графики аппроксимаций - функции

Так как мы аппроксимировали обобщенные функции аналитическим функциями, то мы можем продифференцировать эти аппроксимирующие функции и найти их производные любого порядка. Тем самым мы можем получить приближения производных обобщенных функций с любой степенью точности. Например, аналогично с тем, как это было сделано в предыдущем параграфе, мы можем построить графики приближений производных ─ функции. На рис. 4 изображены графики последовательных аппроксимаций первой, второй и третьей производных - функции.

Таким же образом можно найти и производные более высоких порядков. Построенные графики дают хорошее представление о характере поведения производных - функции. Мысленно увеличивая номер аппроксимирующей функции, по графикам (рис. 4) можно продолжить прослеживаемые тенденции изменения аппроксимаций и представить предельные положения последовательностей функций, аппроксимирующих производные - функции.

Рассмотренный подход поможет улучшить понимание обобщенных функций, являющимися производными - функции, использовать их не просто как абстрактный математический аппарат, а осознанно понимать их структуру, даже если они записаны в предельной форме. Данный подход может быть применим и для лучшего понимания других обобщенных функций и характера их поведения.

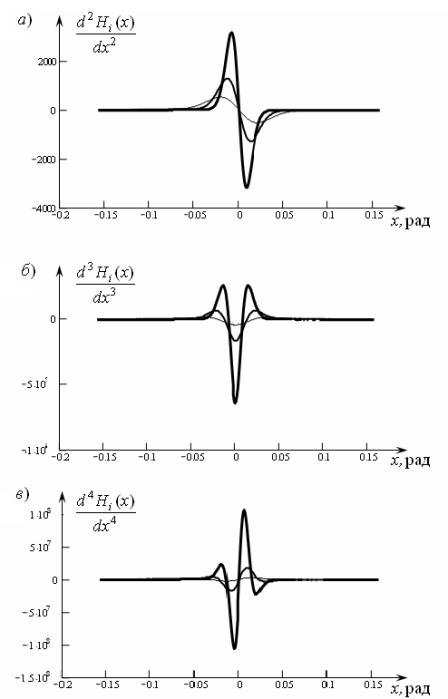
Рис. 4. Графики аппроксимаций производных ─ функции

Известно, что можно аппроксимировать ─ функцию и другими непрерывно дифференцируемыми функциями, например, такими

, ,

, ,

, ,

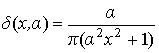для которых и .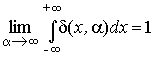

Недостаток аппроксимации ─ функции с помощью третьей из этих функций заключается в высокой погрешности, так как эта функций имеет не только положительные, но и отрицательные значения. Причем последовательность отрицательных значений не ограничена снизу, то есть погрешность может быть сколь угодно большой.

Что касается аппроксимации с помощью первых двух функций, то они позволяют аппроксимировать периодическую ─ функции лишь в виде суммы 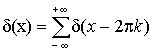, что может быть неудобным для практического использования, тогда как аппроксимирующие функции по предложенному методу являются периодическими по своей природе и позволяют аппроксимировать периодическую ─ функцию без каких-либо дополнительных построений. Примером может служить график функции ,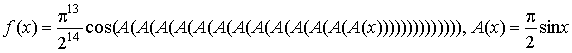

изображенный на рис. 5.

Построенную функцию можно использовать для аппроксимации функции распределения дискретной случайной величины, используя соотношени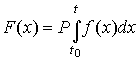е , где ─ параметр, определяемый из свойств функции распределения. Пример так построенной функции распределения приведен на рис. 6.

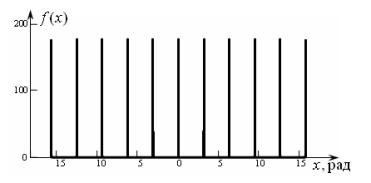
Рис. 5. График функции, аппроксимирующей периодическую

─ функцию

Рис. 6. Пример аппроксимации функции распределения

дискретной случайной величины

Литература

1. Алюков С.В. Аппроксимация ступенчатых функций в задачах математического моделирования // Математическое моделирование, журнал РАН, 2011, том 23, №:3, С.75–88.

2. Alyukov S.V. Approximation of step functions in problems of mathematical modeling // Mathematical models and computer simulations, 2011, vol. 3, № 5, Р. 661 ─ 669.

3. Алюков С.В. Моделирование динамических процессов с кусочно-линейными характеристиками // Известия вузов. Прикладная нелинейная динамика, 2011, том 19, № 5, С. 27 ─ 34.