В.А. Куликова,

кандидат педагогических наук, Заслуженный учитель РФ

Рассудочно-деятельностная технология обучения — основа интеллектуального развития личности

«Ум без разума — беда»

(народная пословица)

Развитие ребёнка идёт не путём развёртывания изнутри готовых, заложенных наследственностью способностей, а в результате усвоения опыта, накопленного предыдущими поколениями. Годы учения в школе — период человеческой жизни, специально отведённый для усвоения основ интеллектуального, этического, умственного, эстетического и других видов социального опыта.

Многое в судьбе ребёнка зависит от того, что он усвоит из этого опыта и как усвоит. Известный физик М. Лауэ в несколько афористической форме дал такое определение образованию: «Образование есть то, что остаётся, когда всё выученное уже забыто». А что остаётся у человека после того, как забыто всё выученное в школе по математике? Сформированность мышления, памяти, внимания, речи и т. д.

Значит, главная задача обучения состоит в том, чтобы сформировать у ребёнка определённые качества, а именно: определённый уровень развития мышления, памяти, внимания, речи, нравственные идеалы.

Богатую пищу для развития мыслительных процессов и ума учеников даёт математика и, в частности, геометрия. Поэтому учителю при изучении математики школьниками необходимо, прежде всего, обращать внимание на развитие их умственных способностей. Сила ума — в его глубине, гибкости, самостоятельности. Слабость ума — в поверхностности, подражательности, инертности, несамостоятельности.

Как же в действительности учителя математики развивают ум школьников? Приведу пример с уроков по теме «Теорема Пифагора». Первый урок по данной теме проводит учитель, который любит объяснять сам, красиво выполнять чертежи на доске. Этот учитель вычерчивает прямоугольный треугольник, объясняет, что он замечательный тем, что в нём сумма квадратов двух меньших сторон (катетов) равна квадрату большей стороны (гипотенузы). Далее учитель доказывает теорему. Учащиеся выполняют чертёж, записывают доказательство теоремы в своих тетрадях. Все работают активно. Но какая польза от этой работы? На таком уроке ученик может лишь запомнить, рассказать новые сведения, подражая учителю.

Ни о какой глубине, гибкости, самостоятельности ума в этом случае не может быть и речи. Делай, как Марья Ивановна, заучивай, запоминай. Объяснение материала рассчитано на память ученика, а не на развитие его умственных способностей. Л.Н. Толстой о таком обучении писал следующее: «Если ученик в школе не научится сам ничего творить, то в жизни он всегда будет только подражать, копировать, так как мало таких, которые бы, научившись копировать, умели сделать самостоятельное приложение этих сведений».

Второй урок проводит учительница, которая убеждена, что ученики должны самостоятельно получать знания с помощью учебника. Она предлагает детям изучить материал самостоятельно по учебнику. А затем, повторив с учениками вывод нового для них свойства прямоугольного треугольника и показав треугольник на красочно оформленном плакате, предлагает учащимся решать задачи на применение теоремы Пифагора. Вроде бы так же, как и на первом уроке, все ученики работают активно, повторяют, запоминают вывод, применяют новые знания практически в решении задач.

Однако и в этом случае учитель не достигает желаемого результата. Во-первых, в учебнике не указываются истоки понятия, закона, его значимости. А во-вторых, при работе с учебником ученик заучивает материал в готовом виде. Работает только его память. Он воспроизводит чертёж, доказательство, вывод так, как это показано в учебнике. А почему так, а не иначе? И если продемонстрировать прямоугольный треугольник в другом положении, то он может показаться ученику и не прямоугольным, потому что в учебнике чертёж другой.

И вновь вопрос: о каком развитии глубины, гибкости, самостоятельности ума может идти речь? Именно так «формируют» «глупых людей», т.е. людей с атрофированной способностью суждения. Зубрёжка, подкрепляемая бесконечным повторением (которое здесь следовало бы назвать не матерью, а мачехой учения), калечит мозг и интеллект тем вернее, чем «умнее сами по себе усваиваемые истины».

«Искалечить орган мышления гораздо легче, чем любой другой орган человеческого тела, а излечить его очень трудно. А позже — и совсем невозможно», — отмечал Э.В. Ильенков.

Именно учитель математики имеет, пожалуй, преимущество перед другими учителями в возможности «калечить мозг учеников», заставляя их заучивать математические истины без понимания, без смысла, а задачи решать без осознания сущности проводимых действий и операций.

Работа учителей математики по объяснению учебного материала имеет смысл лишь в той степени, в какой она служит развитию разума, а не памяти.

Как, к примеру, видится мне последовательность в изучении с учащимися темы «Теорема Пифагора». Необходимо приучить их мыслить самостоятельно, видеть в изучаемом материале главное, находить правильные связи между новыми элементами истины. Поэтому я предлагаю ученикам на отдельных листах бумаги начертить прямоугольный треугольник. Ребята работают по группам-рядам. Первая группа вычерчивает прямоугольный треугольник так, чтобы вершина прямого угла находилась вправо от его остальных вершин; вторая группа строит прямоугольный треугольник так, чтобы вершина прямого угла была расположена влево от его остальных вершин; третья группа строит прямоугольный треугольник с учётом того, чтобы вершина прямого угла находилась выше всех его остальных вершин.

Трое учеников (лучше слабые) от каждой команды вычерчивают прямоугольные треугольники на доске. Почему у доски работают слабые ученики? Да потому что у них списывать другие не станут. Все будут думать сами. Почему вычерчивают фигуры на доске? Для того, чтобы ученики видели порядок и последовательность работы. А иначе начинаются переспрашивания, и создаётся шум. А так работают все спокойно.

Поощряются те ученики, которые сумеют выполнить свой чертёж лучше других. Команды и сами ученики получают за это очки — треугольнички. Начерченные фигуры на доске выглядят, к примеру, так:

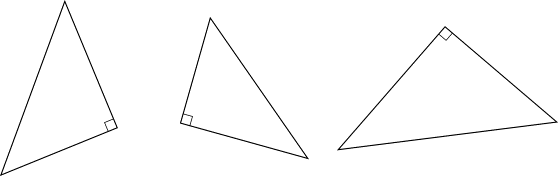
Рис. 1

Поскольку чертежи выполнены на доске, то ребята наглядно видят различные положения прямоугольного треугольника.

Конечно, всегда есть ученики, которые справляются с этими заданиями очень быстро. Поэтому, чтобы они не «бездельничали», необходимо предложить им изобразить положение прямоугольного треугольника, отличного от того, который они выполнили, и тем самым сделать как можно больше разнообразных чертежей.

Самый «умный ученик» выполняет чертежи на настольной доске (планшетке) для того, чтобы потом показать их всему классу.

Первый этап проведён.

Далее учащимся предлагается записать названия сторон прямоугольного треугольника, с помощью линейки измерить длину его сторон, возвести их в квадрат и сравнить.

«Что можно при этом заметить, какую зависимость? — спрашивает учитель. Если ученики затрудняются ответить, то неплохо вспомнить с ними свойства сторон треугольника. Для этого стоит задать им, скажем, такие вопросы:

«Когда три отрезка могут образовать треугольник?»,

«Можем ли мы также сравнить суммы квадратов двух сторон?»,

«Какой вывод из этого следует сделать?».

Поощряются учащиеся, которые точнее и аккуратнее других выполняют эту работу и получают притом результат с наименьшей абсолютной погрешностью.

Но вывод ещё не формулируется, потому что практическая работа не закончена. Учащимся предлагается на каждой стороне прямоугольного треугольника построить квадрат, вырезать эти квадраты и наложить их так, чтобы два меньших квадрата уложились в большем.

«Наука утверждает, — говорит учитель, — что это возможно». И вновь поощряются те, кто смог выполнить данную работу. Ясно, что вместе с учениками поощрения заслуживают и их команды, поэтому урок проходит в игровой форме, дети работают с большим желанием.

Затем учитель рассказывает о применении свойств треугольника со сторонами 3; 4; 5 в Египте. «Почему египтяне использовали такой треугольник для измерения площади своих полей?», — спрашивает он учеников. На плакате красочно нарисован египетский треугольник на фоне пальм. Учащимся предлагается проделать такую же работу со сторонами египетского треугольника, и они возводят в квадрат стороны, получают числа 9; 16; 25. Сравнивают результаты. Догадываются, что египетский треугольник — прямоугольный. Египтяне с помощью такого треугольника строили прямые углы и измеряли площади полей в форме прямоугольников.

Формулируются две теоремы: прямая и обратная. Рассматриваются их сходство и различие.

Обычно вывод — формулировку теорем ученики запоминают непроизвольно, так как математический закон стал для них собственным открытием.

С доказательством теоремы торопиться не следует. Главное, чтобы ученики пришли к пониманию нового математического закона, как собственного открытия, и у них бы возник интерес к новым знаниям. Далее учитель продолжает рассказ из истории возникновения теоремы Пифагора. Говорит о том, что впервые теорема была доказана Пифагором, рассказывает о жизни Пифагора и его школе, показывает юмористические рисунки на эту тему. Рассматривая их, ученики устанавливают связь с площадями квадратов, построенных на гипотенузе и на катетах.

«Существует, — говорит учитель, — более 200 способов доказательства этой теоремы. В разных учебниках приводятся разные способы её доказательства». Для наглядности учитель показывает на плакате несколько рисунков, применяемых для доказательства теоремы Пифагора. Ученикам предлагается выбрать один из них и объяснить доказательство. Если ученики затрудняются, то учитель сам подсказывает способ доказательства, но делает это в форме рассуждений и диалога с учащимися. И только после такого разбора рекомендуется прочитать материал учебника, сравнить полученные выводы с выводами, записанными в учебнике.

Иногда учителя сетуют на то, что на одном уроке не хватает времени для таких тщательных рассуждений по изучению нового материала. Если это так, то можно на первом уроке не доказывать теорему — доказательство ещё не главное. Главное — получить самостоятельно закон, рассмотреть его практическое применение. Поэтому после получения вывода о свойстве прямоугольного треугольника можно закрепить этот закон решением практических задач.

На следующем же уроке после повторения формулировки теоремы Пифагора с помощью устного решения задач стоит провести доказательство теоремы. Лучше доказывать её не одним способом. Для этого желательно предложить сильным ученикам несколько способов доказательства по рисункам на плакате, а затем их рассуждения заслушать всем классом.

Вариантов дальнейшей работы над изучением теоремы Пифагора может быть несколько, но самое главное в изучаемом материале дети уже знают.

Не нужно предлагать учащимся заучивать доказательства теоремы без усвоения основной идеи, логики его проведения. Если ученик стремится запомнить каждый шаг вывода, каждое обозначение, каждое дополнительное построение вместо того, чтобы разобраться, зачем оно делается и в чём состоит связь звеньев рассуждения, то при таком подходе он взваливает на себя непосильный труд, не развивая своего мышления. О таком человеке говорят: много знает, но мало понимает.

Нельзя преуменьшать и того обстоятельства, что беседы учителя с учащимися по истории науки представляют богатейшие возможности для возбуждения их творческих сил, для развития мышления. Хорошо подобранными примерами из жизни учёных можно показать, как много неизвестного окружает нас, находится рядом с нами, но мы только этого не замечаем, поскольку слишком привыкли к окружающему и не можем взглянуть на него с новых, непривычных позиций.

Таким образом, социальная значимость аспекта образования с помощью математики заключается в повышении средствами математики уровня интеллектуального развития человека.

Рассудочная самодеятельность школьника позволяет ему осознать те факты, те законы природы, которые он познаёт.

Литература:

1. Выготский Л.С. Педагогическая психология. М.: «Педагогика», 1991.

2. Психологические основы формирования личности в педагогическом процессе. — М.: «Педагогика», 1981.

3. Куликова В.А. Чтобы урок был не в тягость, а в радость, или как работать без отстающих: Кн. для учителя: из опыта работы. — Тюмень: Поиск, 1997. — 95 с.