Разина О.В., Цыба П.Ю.
Евразийский национальный
университет им. Л.Н. Гумилева, Астана, Казахстан
Космологическое
ускорение в модели g-эссенции
Более десяти лет спустя после своего открытия
[1], космическое ускорение остается нерешенной проблемой. В литературе были
предложены, некоторые теоретические модели, ответственные за это ускоренное
расширение. Простейшей моделью является космологическая постоянная, которая
является ключевым компонентом в 
модели, но данная
модель сталкивается с проблемой тонкой настройки.
В последние годы в теории описываются модели
k-эссенции, с неканоническими кинетическими членами. Такие теории были впервые
изучены в контексте k-инфляции [2], а затем модели k-эссенции были предложены в качестве динамической
темной энергии для решения проблемы космического совпадения [3].
Совсем недавно была представлена фермионная контрпара
скалярной k-эссенции в [4] и названа для краткости f-эссенция. В [4], была
предложена еще более общая модель темной энергии, так называемая g-эссенция
(см. [5]-[7]).
Действие для g-эссенции записывается как [8]
, (1)
где
K является некоторой функцией своих
аргументов, 
– скалярная функция, 
является фермионной
функцией и 
ее сопряженная
функция. Здесь
, 
являются
каноническими кинетическими членами для скалярного и фермионного полей,
соответственно. 
и 
являются ковариантными
производными. Фермионные поля рассматриваются здесь как классические
коммутирующие поля.
Варьирование действия (1) относительно 
дает нам следующий
тензор энергии-импульса для поля g-эссенции
где 
, 
, 
и т.д. Уравнение
движения для скалярного поля 
получается
варьированием действия (1) относительно 
.
Варьируя
действие (1) относительно 
мы получим уравнения
Эйнштейна
,
где
является тензором
Риччи. Кроме того, из уравнения Эйлера-Лагранжа относительно плотности
лагранжиана K можно получить
уравнения Дирака для фермионного поля 
и его сопряжения 
связанного с
гравитационным и скалярным полями.
Рассмотрим однородную, изотропную и плоскую
Вселенную Фридмана–Робертсона– Уокера (ФРУ) заполненную g-эссенцией. Метрика задается
в виде
,
(2)
и
тетрадный базис выбран
, 
В целом, модель
g-эссенции (1) может иметь очень сложные уравнения движения и поиск ее точных
аналитических решений является трудной задачей. Здесь мы рассмотрим более простую
модель следующего вида
,
где
. Тогда уравнения соответствующие действию (1) запишутся как [8]
, (3)
, (4)
, (5)
, (6)
, (7)
, (8)
где
, 
.
Рассмотрим случай 
и вычислим некоторые
точные решения. Тогда система (3)-(8)
примет вид
,
(9)
, (10)
, (11)
, (12)
, (13)
, (14)
где
, 
.
Решая
эту систему получим следующие решения
, 
, 
и
, 
.
Здесь
, 
и 
удовлетворяет
следующему условию 
и 
.
Теперь найдем точное решения (9)-(14). Это
решение имеет интересное свойство: оно периодически пересекается с фантомной
линией 
. Для этого решения рассмотрим в деталях физические свойства,
такие как давление p, плотность энергии ρ, скалярный потенциал и особенно
поведение УС.
Будем исходить из следующего выражения для
масштабного фактора
,
где
, b, d, k
являются
константами. Тогда получим
,
, 
,
, 
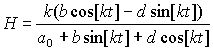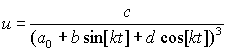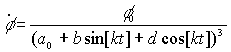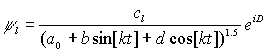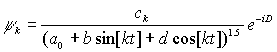
где
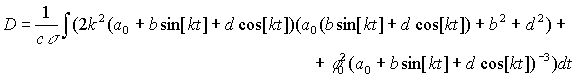
Соответствующий
потенциал имеет форму
.
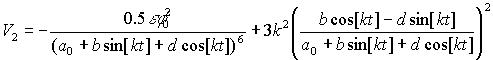Плотность
энергии и давление имеют форму
,
.
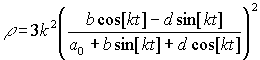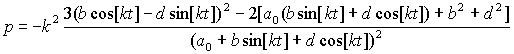Параметр
уравнения состояния и параметр замедления имеют вид
,
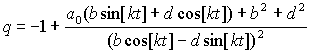
На
рисунке 1 а) представлены графики для плотности энергии 
и давления 
как функций от 
. На рисунке 1 b) представлен график
параметра УС 
как функции от 
.
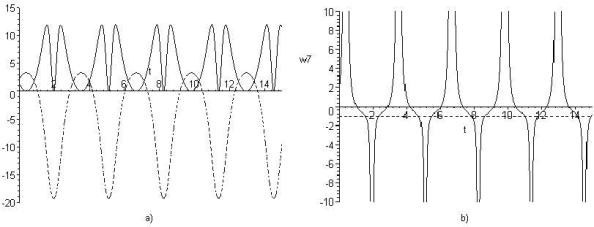
Рис. 1. а) Графики 
(сплошная линия) и 
(пунктирная линия)
как функций от 
;
b)
График 
как функции от 
(a0=2; b=1; d=1; k=2).
При этом параметр рывка равен
.
На рисунке 2 представлены графики параметра
замедления 
и параметр рывка 
как функций от t, соответственно.
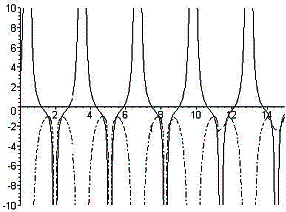
Рис.
2. График 
(сплошная линия) и 
(пунктирная линия)
как функций от t (a0=2; b=1;
d=1; k=2).
В этой статье мы рассмотрели новую и интересую
модель, так называемую g-эссенцию. Эта
модель объединила k-эссенцию и f-эссенцию, которые были изучены ранее.
Вывели уравнения поля для лагранжиана общего вида. Ввели феноменологический
лагранжиан, в котором уравнения поля имеют простой вид. Нашли точное фантомное решение. Найдены
точные решения уравнения, а также выражения для давления и плотности энергии,
как функций от времени.
Литература:
1. Perlmutter
S. // Astrophys.J. – 1999. – V.517. – P.565–586; Riess A. // Astron.J. – 1998. – V.116 – P.1009–1038.
2. Armendariz-Picon C., Damour T.,
Mukhanov V.F. k-inflation // Phys. Lett. B. – 1999. – V.458. – P.209-218
[hep-th/9904075].
3. Armendariz-Picon C., Mukhanov V.F., Steinhardt P.J. Essentials of
k-essence // Phys. Rev. D. – 2001. – V.63. – P.103510 [astro-ph/0006373].
4. Myrzakulov
R. Fermionic k-essence // [arXiv:1011.4337].
5. Yerzhanov
K. K, Tsyba P. Yu, Myrzakul Sh. R, Kulnazarov I. I, Myrzakulov R. Accelerated expansion
of the Universe driven by G-essence // [arXiv:1012.3031].
6. Kulnazarov
I, Yerzhanov K, Myrzakul Sh, Tsyba P, Myrzakulov R. G-essence with Yukawa
Interactions // European Physical Journal C. – 2011. – V.71, N7. – P.1698 (9p) [arXiv:1012.4669].
7. Razina O, Kulnazarov
I, Yerzhanov K, Tsyba P. Yu, Myrzakulov R. Einstein-Cartan gravity and
G-essence // Central European Journal of Physics. – 2012. – V.10, N1. – P.47-50 [arXiv:1012.5690].
8. Jamil M, Momeni D,
Serikbayev N. S, Myrzakulov R. // Astrophysics and Space Science. – 2012. –
DOI: 10.1007/s10509-011-0964-7 (Preprint arXiv:1112.4472); Jamil M, Myrzakulov Y, Razina O, Myrzakulov R. //
Astrophysics and Space Science. – 2011. – V.336. – P.315-326.