Строительство и архитектура/3. Современные технологии строительства, реконструкции и реставрации

Ст-т Марсов А.А.; к.т.н. Кузнецова С.Г.

Пермский национальный исследовательский политехнический университет, Россия

ОПРЕДЕЛЕНИЕ СМЕЩЕНИЯ ОПОРНОГО СЕЧЕНИЯ ДВУХШАРНИРНОЙ АРКИ ПРИ УСЛОВИИ

В двухшарнирной арке (рис. 1) определим смещение правой опоры B, при котором максимальный изгибающий момент был бы равен минимальному изгибающему моменту по абсолютной величине. Момент инерции сечения арки изменяется по закону , где - момент инерции в ключе. Арка очерчена по параболе .

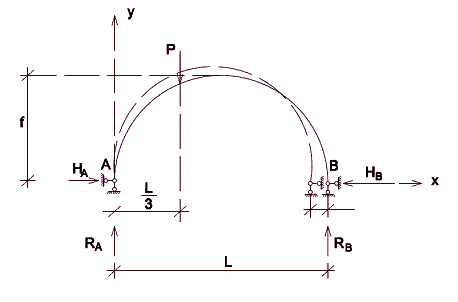
Рис. 1

Для расчета используем метод сил. Основная система показана на рис. 2, а.

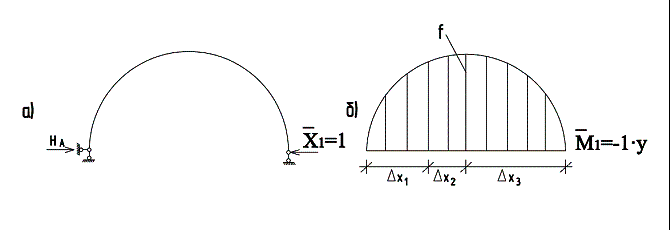
Рис. 2

Каноническое уравнение: . Отсюда ,

где y – ордината сечения, выполняющая роль единичного изгибающего момента (рис. 2, б);

– грузовая эпюра изгибающих моментов (рис. 3);

- длина интервала, полученного разбиением единичной и грузовой эпюр изгибающих моментов.

Рис. 3

Разобьем эпюры и на три неравных интервала: ; ; , тогда .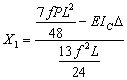

Строим окончательную эпюру изгибающих моментов (рис. 4) по формуле: . На основании этой формулы имеем: ; .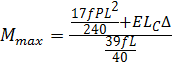

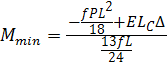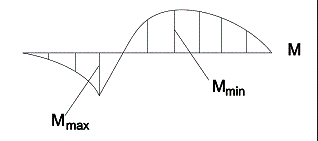
Рис. 4

Приравнивая абсолютные значения и , находим : .

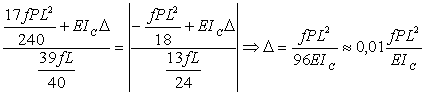Таким образом, в двухшарнирной арке от сосредоточенной силы , находящейся от левой опоры на расстоянии , при выполняется условие . При таком подходе расчета можно регулировать распределение усилий в двухшарнирной арки при смещении опор, что является актуальным в расчетах двухшарнирных систем.

Литература:

1. Строительная механика. Основы теории с примерами расчетов: Учебник/Под ред. А.Е. Саргсяна – 2-е изд., испр. и доп. – М.: Высш. шк., 2000 – 416 с.