Ковалец О.Я.

Национальный технический университет Украины «КПИ»

ОПРЕДЕЛЕНИЕ РАДИУСОВ КРИВИЗНЫ ПОПЛАВКОВОГО ПОДВЕСА СПЕЦИАЛЬНОЙ ФОРМЫ

Для вычисления радиусов кривизны используются соотношения Гаусса-Кодацци: соотношение Гаусса –

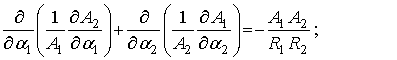(1)

соотношения Кодацци –

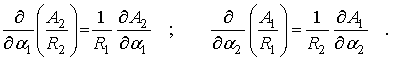(2)

Величины А₁, А₂, R₁, R₂ не могут быть заданы как произвольные функции точки поверхности. Они должны удовлетворять равенствам (1), (2). Из теории поверхностей известно, что задание этих четырех величин в виде приведенных соотношений, полностью определяет поверхность (с точностью до положения ее в пространстве).

В линиях кривизны правила дифференцирования ортов записываются в виде:

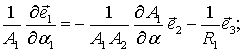
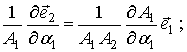
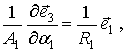(3)

здесь - орт нормали к поверхности.

Запишем формулы для вычисления кривизны координатных линий и при недеформированном состоянии поверхности поплавка. Уравнение для точек срединной поверхности оболочки вращения имеет вид:

(4)

Из формул (3) следует:

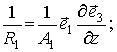
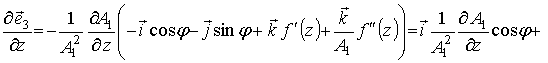
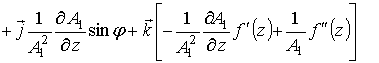. (5)

Тогда,

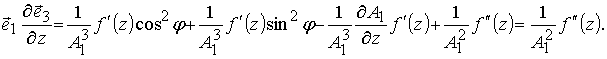
С учетом полученного, можно записать известное соотношение –

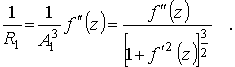(6)

.

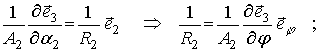
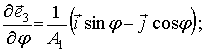
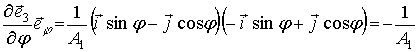Таким образом, 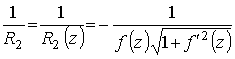. (7)

Если оболочка вращения представляет собой цилиндрическую поверхность, тогда где R – радиус оболочки. В этом случае

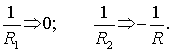
Представляет интерес, каким образом изменится тождество Кодацци для рассматриваемой оболочки вращения:

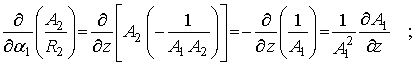
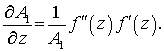
Уточним соотношения для вычисления параметров А_1, А₂, а также кривизн. Проводя дальнейшие исследования, принимаем обязательным выполнение

условия – . Параметр А₂ целесообразно представить в виде-

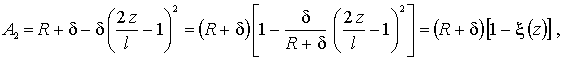(8)

Параметр А₁ представим в виде –

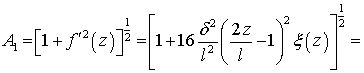
Окончательно значение параметра А₁ запишем так :

В дальнейшем считаем геометрию оболочки такой, для которой выполняется условие –

Преобразуем соотношения для вычислений величин и . Имеем:

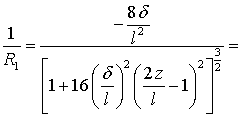
(9)

С учетом основных допущений последнее выражение упрощается:

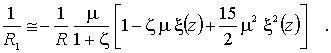(10)

Найдем значение кривизны :

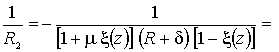
(11)

Окончательно имеем:

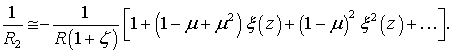
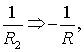Если получаем что и должно иметь место.