К.т.н. Дмитриев А.В., д.т.н. Нуруллин Э.Г., к.т.н. Халиуллин Д.Т.

Казанский государственный аграрный университет, Россия

ОБОСНОВАНИЕ ФОРМЫ ЛОПАСТИ ВЕНТИЛЯТОРА БРОСКОВОГО ТИПА

В машинах для пневмомеханического шелушения зерна крупяных культур в качестве разгонного устройства для перерабатываемого продукта используется горизонтально установленный вентилятор броскового типа, лопасти ротора которого имеют криволинейную форму [1, 2]. Для обоснования формы лопасти вентилятора броскового типа необходимо, прежде всего, рассмотреть движение зерновки по ней и силы, действующие на зерновку во время движения (рисунок 1).

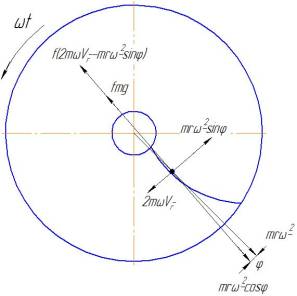
Рисунок 1. Силы, действующие на зерновку при ее движении по криволинейной лопасти броскового вентилятора.

При рассматриваемом движении на зерновку действуют силы:

а) сила тяжести - . При горизонтальном положении диска и вертикальном положении лопатки проекции этой силы в плоскости диска и лопатки равны нулю.

б) центробежная сила -

в) сила трения частицы по поверхности диска - Так как зерновка перемещается в относительном движении в плоскости лопатки, то эта сила также будет направлена по касательной к выгнутой плоскости лопатки;

г) сила Кориолиса. Величина этой силы равна где - скорость относительного движения зерновки;

д) сила трения частицы по поверхности лопатки - Возникновение этой силы сопряжено с наличием давления зерновки на поверхность лопатки;

Действие вышеперечисленных сил на зерновку при ее движении по криволинейной поверхности лопатки рассмотрено П.М. Василенко. На основе анализа этих сил им было выведено дифференциальное уравнение углового перемещения материальной частицы по криволинейной лопасти:

(1)

где j - угловое перемещение частицы в относительном движении.

Для определения уравнения кривой лопасти броскового вентилятора воспользуемся вышеуказанным дифференциальным уравнением углового перемещения материальной частицы в относительном движении.

Уравнение кривой лопасти броскового вентилятора должно представлять собой уравнение связи для выражения (1). Только в этом случае дифференциальное уравнение углового перемещения частицы будет разрешимо.

П.М. Василенко предложил уравнение кривой, представляющее собой уравнение логарифмической спирали:

(2)

где r₀ – начальное значение координаты r;

j - полярная координата;

– постоянная величина.

при этом он выразил как . Применение этого условия дает возможность решения уравнения (1).

Однако можно выразить и другим способом:

(3)

В этом случае решение уравнения (1) возможно с применением иного уравнения кривой лопасти.

Поставим задачу найти уравнение кривой горизонтального сечения лопатки броскового вентилятора, применяя условие (3), которое можно записать в следующем виде:

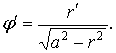(4)

Дифференцируя уравнение (4) получим:

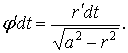(5)

Решаем уравнение (5):

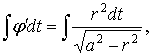
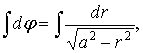
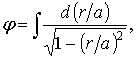
(6)

Постоянную можно приравнять нулю, вследствие чего получаем:

(7)

где

Полученное уравнение – полярное уравнение окружности. Заметим, что в прямоугольной системе координат это же уравнение записывается в виде:

(8)

Таким образом, в результате анализа дифференциального уравнения углового перемещения материальной частицы по криволинейным лопастям получено выражение, описывающее форму лопасти броскового вентилятора, на основе которого она может быть построена.

Литература:

1. Патент на полезную модель 91892 РФ, МПК В02В 3/00. Устройство для шелушения зерна /Э.Г. Нуруллин, А.В. Дмитриев, Д.Т. Халиуллин, И.В. Маланичев – Опубл. 10.03.2010. Бюл. № 7.

2. Дмитриев А.В. Разработка и исследование пневмомеханического шелушителя: дис. … канд. техн. наук, - Казань, 2003.