Куанбай Н, Битибаева А, Тургунова М.
Дифференциальный оператор второго порядка с
инволюцией на всей
числовой оси. Обратный оператор
Южно-Казахстанский
государственный университет им.М.Ауезова
Следуя Т.Като [1.с.520] можно
рассмотреть обобщенную спектральную задачу
![]() ,
,
где ![]() и
и ![]() линейные операторы
в гильбертовом пространстве
линейные операторы
в гильбертовом пространстве ![]() . Если
. Если
![]()
то имеем обобщенную спектральную задачу
![]()
![]()
Если же оператор ![]() определить равенством
определить равенством
![]()
для любой функции ![]() , то получим
одномерное дифференциальное уравнение второго порядка с инволюцией
, то получим
одномерное дифференциальное уравнение второго порядка с инволюцией
![]() (1)
(1)
Изучению дифференциальных уравнений с инволюцией посвещены
работы очень многих авторов [см., например,2-3].
Цикл работ А.П.Хромова и его последователей [см., например, 4], М.А.Садыбекова
и А.М.Сарсенби [5-7] содержат
результаты исследований по спектральным свойствам дифференциальных уравнений с
инволюцией.
Отметим,
что в работе [8] детально изучены вопросы дискретности спектра и полноты
собственных и присоединенных функции обыкновенного дифференциального уравнения
![]()
а в работе [9] получены условия
безусловной базисности в ![]() системы собственных
и присоединенных функций этой спектральной задачи.
системы собственных
и присоединенных функций этой спектральной задачи.
Рассмотрим
уравнение (1), где комплекснозначный коэффициент ![]() есть функция, суммируемая на каждом конечном
интервале числовой оси. Пусть
есть функция, суммируемая на каждом конечном
интервале числовой оси. Пусть ![]() для
для ![]() . Любую функцию
. Любую функцию ![]() из класса
из класса ![]() , которая абсолютно непрерывна вместе со своей первой
производной на каждом конечном интервале числовой оси и при некотором значении
комплексного параметра λ почти всюду в ней удовлетворяет уравнению (1),
будем называть собственной функцией спектральной задачи (1). Этим определением описывается область
определения оператора
, которая абсолютно непрерывна вместе со своей первой
производной на каждом конечном интервале числовой оси и при некотором значении
комплексного параметра λ почти всюду в ней удовлетворяет уравнению (1),
будем называть собственной функцией спектральной задачи (1). Этим определением описывается область
определения оператора
![]() ,
, ![]()
![]() ≥1. Другими словами область определения оператора
≥1. Другими словами область определения оператора ![]() состоит, из функций
состоит, из функций ![]() абсолютно
непрерывных вместе со своей первой производной на каждом конечном интервале
числовой оси, и удовлетворяющих условию
абсолютно
непрерывных вместе со своей первой производной на каждом конечном интервале
числовой оси, и удовлетворяющих условию
![]()
Заметим, что если ![]() , то ввиду симметричности рассматриваемого промежутки,
, то ввиду симметричности рассматриваемого промежутки, ![]() также принадлежит
классу
также принадлежит
классу ![]() .
.
Если заменить в уравнении (1) ![]() на
на ![]() то получим обычную
спектральную задачу
то получим обычную
спектральную задачу
![]()
для дифференциального оператора
![]() .
.
Ясно, что ![]() для
для ![]() . Области определения операторов
. Области определения операторов ![]() и
и ![]() совпадают.
совпадают.
В следующей теореме покажем плотность области определения
оператора ![]() в классе
в классе ![]()
Теорема 1. Если
![]() , то число λ=0 не является собственным значением
оператора
, то число λ=0 не является собственным значением
оператора ![]() .
.
Доказательство. Допустим противное. Пусть собственному значению λ=0
соответствует собственная функция ![]() , т.е.
, т.е.
![]() .
.
Обе части этого уравнения умножим на
комплексно сопряженную функцию ![]() и проинтегрируем на
некотором интервале
и проинтегрируем на
некотором интервале ![]()
![]() 0.
0.
Проинтегрируем первое слагаемое
по частям.
![]() 0
0
или

Рассмотрим вещественную часть последнего уравнения.
![]()
(2)
Далее, во первых,
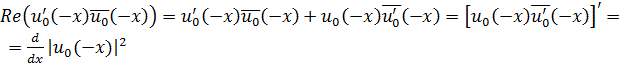
(3)
Во-вторых, условие ![]() означает, что
функция
означает, что
функция ![]() не отделена от нуля
на любом бесконечном промежутке. Значит, существуют последовательности
не отделена от нуля
на любом бесконечном промежутке. Значит, существуют последовательности ![]() , такая то
, такая то ![]() , и последовательность
, и последовательность ![]() , такая, что
, такая, что ![]()
Перепишем равенство (2) в виде
![]() (4)
(4)
С учетом (3) и сделанных замечаний, заключаем что все
слагаемые в левой части равенства (4) положительны. Тогда предельный переход по
последовательностям ![]() и
и ![]() дает равенство
дает равенство


Отсюда следует ![]() . Тогда
. Тогда ![]() . Теорема доказана.
. Теорема доказана.
Рассмотрим сужение ![]() оператора
оператора ![]() . Область определения
. Область определения ![]() сужения
состоит из финитных функций
сужения
состоит из финитных функций ![]() , каждая из которых абсолютно непрырывна вместе со своей первой
производной.
, каждая из которых абсолютно непрырывна вместе со своей первой
производной.
На
![]() действие оператора
действие оператора ![]() совпадает с действием оператора
совпадает с действием оператора ![]() , т.е.
, т.е.
![]()
для любой функции ![]() . Совокупость функций
. Совокупость функций ![]() составляет область значений
оператора
составляет область значений
оператора
![]() .
.
Теорема 2. Множество значении ![]() оператора
оператора ![]() плотно в
плотно в ![]() , тогда и только тогда, когда число
, тогда и только тогда, когда число
![]() не является собственным значением
оператора
не является собственным значением
оператора ![]() .
.
Доказательство.
Достаточность. Пусть число ![]() не является собственным значением оператора
не является собственным значением оператора ![]() . Это означает, что уравнение
. Это означает, что уравнение
![]()
не имеет ненулевого решения
из класса ![]() .
.
Нам
нужно показать плотность множества ![]() в
в ![]() . Допустим противное.
. Допустим противное.
Пусть множество ![]() не плотно в
не плотно в ![]() . Тогда найдется ненулевая функция
. Тогда найдется ненулевая функция ![]() ортогональная всем
элементам множества
ортогональная всем
элементам множества ![]() , т.е.
, т.е.
![]() (5)
(5)
![]()
![]() и
и ![]()
![]() .
.
Пусть ![]() и
и ![]() два линейно независимых
решения уравнения
два линейно независимых
решения уравнения
![]() ,
,
не принадлежащие![]() . Далее, если некоторая функция
. Далее, если некоторая функция ![]() на некотором конечном интервале
на некотором конечном интервале ![]() ортогональна каждой из
функций
ортогональна каждой из
функций ![]() и
и ![]() , т.е.
, т.е.
![]()
![]() , (6)
, (6)
то уравнения
![]()
имеет решение ![]() , такое, что
, такое, что
![]() ,
,
![]() ,
,
где ![]() вронскиан решений
вронскиан решений ![]() и
и ![]() .
.
Функция ![]() будет принадлежать
будет принадлежать ![]() , если продолжить ее на всю числовую ось
нулем. Теперь равенство (5) можно
записать в виде
, если продолжить ее на всю числовую ось
нулем. Теперь равенство (5) можно
записать в виде
![]() (7)
(7)
Из равенства (6) следует
![]()
или
![]() .
.
Последнее равенство сравнивая
с (7), получаем
![]() ,
,
![]() (8)
(8)
Поскольку ![]() -произвольны , а
-произвольны , а ![]() ,
, ![]() -линейно независимы, то равенство
(8) верно для всех
-линейно независимы, то равенство
(8) верно для всех ![]() . С другой стороны равенство (8) показывает, что функция
. С другой стороны равенство (8) показывает, что функция ![]() является решением уравнения
является решением уравнения
![]() .
.
Но функция ![]() , а вместе с ней и функции
, а вместе с ней и функции ![]() ,
, ![]() принадлежат
принадлежат ![]() , следовательно, по условию теоремы
, следовательно, по условию теоремы
![]() . А это противоречит второму
условию (5). Значит, достаточность доказана.
. А это противоречит второму
условию (5). Значит, достаточность доказана.
Необходимость.
Пусть множество ![]() плотно в
плотно в ![]() . Если число
. Если число ![]() является собственным значением оператора
является собственным значением оператора ![]() , то существует функция
, то существует функция ![]() такая, что
такая, что
![]() .
.
Рассмотрим выражение
![]()
где ![]() .
.
Проинтегрерируем по частям два раза слагаемое, содержащее вторую производную.
При этом в силу финитности функции ![]() все внеинтегральные
члены обращаются в нуль. Поэтому мы будем иметь
все внеинтегральные
члены обращаются в нуль. Поэтому мы будем иметь
![]()
Поэтому
равенство
![]()
означает ортогональность ненулевой
функции ![]() к множество
к множество ![]() . Следовательно, множество
. Следовательно, множество ![]() не плотно в
не плотно в
![]() . Полученное противоречие
доказывает теорему.
. Полученное противоречие
доказывает теорему.
Список
использованных источников
1. Като Т., Теория возмущений линейных операторов
-М.: Мир, -1972. –c.740.
2. Wiener J. Generalized solutions of functional differential equations, //Singapore World Sci -Singapore. -1993, с.160-215.
3. Przeworska-Rolewics D., Equations with transformed argument an Algebrais approach// Warszawa. – 1973, р.354.
4. Хромов А.П., Смешенная задача для дифференциального уравнения с инволюцией
и потенциалом специального вида //Изв.Сарат.ун-та.-
2010. -Т.10. - №4. c.17-22.
5. Sadybekov, M.A. and Sarsenbi, A.M., Solution of fundamental spectral
problems for all the boundary value probiems for a first-order differential equation with a deviating argument //Russian, Uzbek.Mat.Zh.-2007. -№3, c.88-94;
6. Sarsenbi, A.M., Unconditional
bases related to a nonclassical second-order differential operator// Russian, Differ.Uravn.46. -2010. -№ 4. –c.506-511
7. Садыбеков М.А., Сарсенби А.М., Критерий базисности системы собственных функций инволюции //Дифференциальное уравнения.
-2012.
–Т.48. -№8. c.1126.
8. Лидский В.Б., Несамосопряженный оператор
типа Штурма-Лиувиля с дискретным спектром //Труды международного мат. общества. -1960, -№ 9. c.45-79.
9. Sarsenbiev, A.M., The property of
being an unconditional basis for the system of eigen-and associated
functions of the one dimensional Schrodinger operator on the entire axis //Russian,
Izv.Akad.Nauk Kazakh.SSR Ser.Fiz.-Mat.
-1989. -№5. p.31-34.