Математика/4. Прикладная математика

Федоренко В.Е., Миленин А.Н., Склярова Н.А.

Харьковский национальный технический университет сельского хозяйства имени Петра Василенко

СПООСОБЫ ВЫПОЛНЕНИЯ ЭЛЛИПТИЧЕСКОГО ПРОЕКТИВНОГО СОООТВЕТСТВИЯ НА ПРЯМОЙ

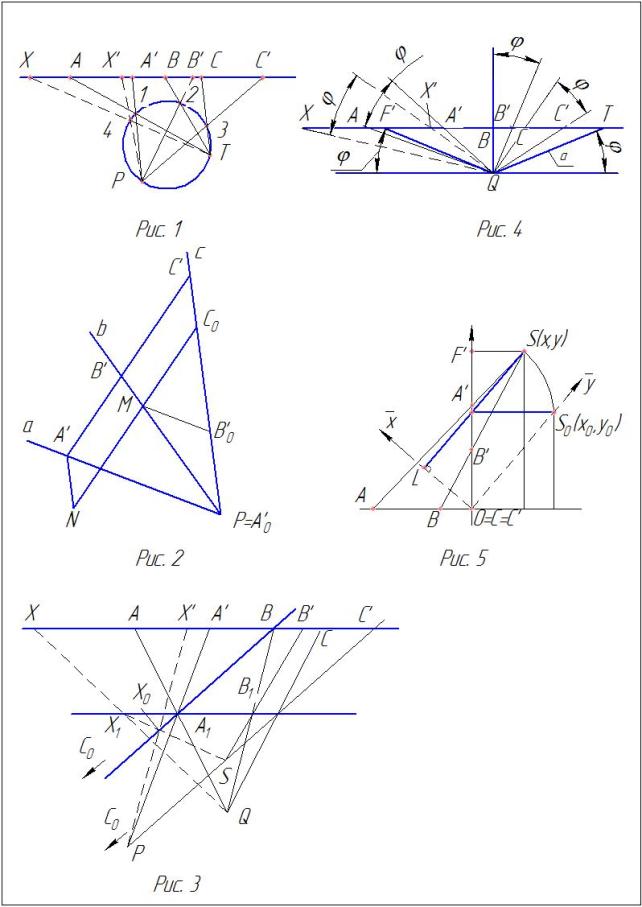
Будем искать точку х' – образ точки х в заданном на прямой эллиптическом проективном соответствии (рис.1).

Прилагаем три способа построения х'

1-й способ. Проецируем тройку А,В,С пучком лучей из произвольного центра Т (рис.1). Подвергаем этот пучок параллельному переносу и получаем конгруэнтный ему пучок лучей с центром Р (рис.2).

Пусть а, b, с – лучи пучка Р. «Насадим» на них тройку А,В,С таким путем.

Переносим тройку А',В',С' на луч "с" в положение А'₀, В'₀,С'₀. Через точку В'₀ проводим прямую, параллельную лучу "а" и отмечаем точку М пересечения этой прямой с лучом "b". Соединяем С'₀ с М прямой и откладываем на ней от С'₀ отрезок С'₀N = С'А'. Через N проводим прямую, параллельную лучу "c" до пересечения с лучом "a" в точке А'. Через А' в направлении N С'₀ проводим прямую, на которой находится тройка А',В',С' , «насаженная на лучи а, b, с.

Это вытекает из того, что

Δ С'₀В'₀М ~ Δ С'А'₀А' и Δ А'₀С'В' ~ Δ А'₀С₀М

Поступаем теперь следующим образом.

Пучок Р переносим с рис.2 на рис.1 с расчетом, чтобы тройка А',В',С' на пучке и на прямой совпали. Пучок Р в этом положении и пучок Т , как два проективных и конгруэнтных пучка, образуют окружность [3] . Они проходят через центры Р, Т и точки 1,2,3 пересечения трех пар соответственных лучей. При помощи этой окружности легко находим точку х' – образ точки х.

2-й способ. Он является практической реализацией известной теоремы, которая гласит: эллиптическое проективное соответствие на прямой можно представить в виде произведения трех перспективных соответствий [1] .

Обозначим через Q‚ S‚ Р центры этих соответствий (рис.2).

Центр Q выбираем произвольно. Из Q мы проецируем А,В,С в тройку А₁,В₁,С₁ второй прямой, параллельной первой.

Проводим теперь прямые А'А₁, В'В₁, С'С₁. Центры "b" и Р получим как точки пересечения прямых А'А₁ и В'В₁ с прямой С'С₁ ,

Пучки с центром Р и S имеют ось перспективы А'В поскольку луч PS двойной.

Имея центр Q,S и Р выполняем три перспективных соответствия в такой последовательности:

Q S P

При этом Х переходит в Х' так

Q S P

3-й способ. Он основан на построении центра, из которого все пары соответственных точек видны под одинаковыми углами, равными φ.

Перейдем к построению этого центра.

Проективное соответствие АВС А'В'С' переводим в перспективное на координатных осях: О_х , О_у (рис. 5). Точка - центр перспективы, а Т и F' – предельные точки. Передвижкой троек можно добиться того, что центр перспективы S перейдет в положение S₀ , равноудаленное от осей координат. В /2/ показано, что переход S в S₀ происходит по равносторонней гиперболе . Точка S₀ – вершина кривой, а оси Ох, Оу – её асимптоты. Зная способ построения вершины гиперболы /2/, мы можем построить S не прибегая к подвижке троек точек.

Проводим сначала оси симметрии гиперболы – прямые , . Теперь проводим две линии: прямую и дугу радиуса LS. Последнее высекает на искомую точку S₀ . Расстояние ее от Ох и Оу одинаковые и равны "à".

Для выполнения эллиптического проективного соответствия на прямой (рис. 4) переносим на эту прямую точки Т и F' с рис. 5. Имея точки Т и F' на прямой, мы проводим из этих точек дуги радиуса "à". Точка их пересечения – искомый центр Q. Точка Х' получается теперь просто.

Проводим луч Qх и поворотом его на угол φ, получаем луч Qх', который высекает на прямой точку Х'. Угол φ берем между лучами, соединяющими центр Q с любой парой соответственных точек.

В заключение отметим, что выбрав один из способов, мы можем использовать два других для контроля.

Литература:

1. Х.С.М. Кокстер–Действительная проективная плоскость.– М., 1959.–с.74

2. Е.П. Дмитренко, В.Е. Федоренко – Приведение проективных рядов во все виды проективного соответствия на прямой. Сб. «Прикладная геометрия и инженерная графика». Вып. 42. Киев, «Будивельник», 1986.

3. Н.Ф. Четверухин – Проективная геометрия. – М., 1963. – с. 184.