М. П. Ленюк
Чернівецький факультет НТУ ”ХПІ”
СКІНЧЕННЕ ГІБРИДНЕ
ІНТЕГРАЛЬНЕ ПЕРЕТВОРЕННЯ ТИПУ БЕССЕЛЯ-ФУР’Є-ЛЕЖАНДРА НА СЕГМЕНТІ ![]() З ДВОМА ТОЧКАМИ СПРЯЖЕННЯ
З ДВОМА ТОЧКАМИ СПРЯЖЕННЯ
Побудуємо інтегральне
перетворення, породжене на множині![]() гібридним диференціальним
оператором (ГДО).
гібридним диференціальним
оператором (ГДО).
![]()
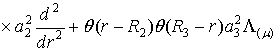 (1)
(1)
У рівності (1) ![]() - одинична функція Гевісайда [1],
- одинична функція Гевісайда [1], ![]() - диференціальний оператор Бесселя [3],
- диференціальний оператор Бесселя [3], ![]() - диференціальний оператор Фур’є [2],
- диференціальний оператор Фур’є [2], ![]() - диференціальний оператор Лежандра
[4]:
- диференціальний оператор Лежандра
[4]:
Означення: Областю задання
ГДО ![]() назвемо множину G вектор-функцій
назвемо множину G вектор-функцій ![]() з такими властивостями:
з такими властивостями:
1)
вектор-функція ![]() неперервна на
неперервна на ![]() ;
;
2)
функції ![]() задовольняють крайові
умови
задовольняють крайові
умови
![]() (2)
(2)
3) функції
![]() задовольняють умови
спряження
задовольняють умови
спряження ![]()
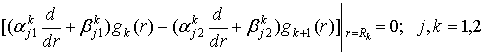 (3)
(3)
Припускаємо, що виконані умови на коефіцієнти:
![]()
![]()
![]()
Зазначимо, що з умов спряження
(3) для ![]() та
та ![]() випливає базова
тотожність:
випливає базова
тотожність:
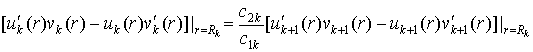 (4)
(4)
Визначимо числа

вагову функцію
![]()
![]() (5)
(5)
та скалярний добуток
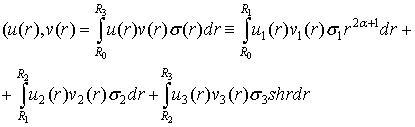
![]() (6)
(6)
Переконаємося, що справджується рівність
![]() (7)
(7)
Згідно правила (6) маємо:

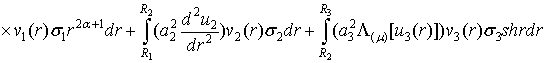 (8)
(8)
Проінтегруємо під знаками
інтегралів два рази частинами:
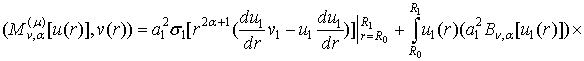
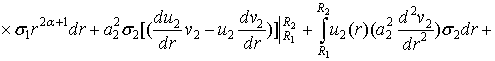
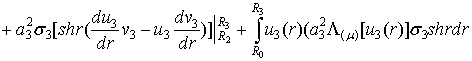 (9)
(9)
Якщо
![]() то
то
![]()
![]() (10)
(10)
Якщо ![]() то
то
![]()
![]() (11)
(11)
В точці спряження ![]() внаслідок базової тотожності (4) при
внаслідок базової тотожності (4) при ![]() знаходимо, що
знаходимо, що
![]()
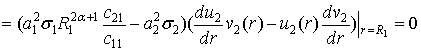 (12)
(12)
тому, що в
силу вибору чисел ![]() та
та ![]() вираз
вираз
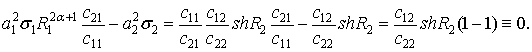
В точці спряження ![]() внаслідок базової
тотожності (4) при
внаслідок базової
тотожності (4) при ![]() знаходимо, що
знаходимо, що
![]()
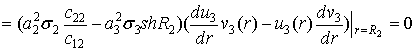 (13)
(13)
тому, що в силу вибору чисел ![]() та
та ![]() вираз
вираз
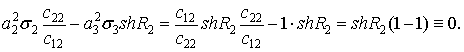
Внаслідок рівностей (10)-(13)
позаінтегральні доданки в рівності (9) рівні нулю. Об’єднуючи інтеграли, що
залишилися, отримуємо рівність (7)
Наявність
рівності (7) означає, що ![]() самоспряжений. Оскільки ГДО
самоспряжений. Оскільки ГДО ![]() на множині
на множині ![]() не має особливої
точки, то спектр ГДО
не має особливої
точки, то спектр ГДО ![]() дійсний і дискретний [6]. Власні елементи ГДО
дійсний і дискретний [6]. Власні елементи ГДО ![]() знайдено як ненульовий
розв’язок породженої ГДО
знайдено як ненульовий
розв’язок породженої ГДО ![]() спектральної задачі
Штурма-Ліувілля.
спектральної задачі
Штурма-Ліувілля.
Припустимо,
що ![]() -спектральний параметр (власне число ГДО
-спектральний параметр (власне число ГДО ![]() ), а функції
), а функції ![]() - компоненти спектральної вектор-функції
- компоненти спектральної вектор-функції
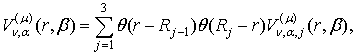 (14)
(14)
яка відповідає власному
числу ![]() .
.
Функції ![]() повинні задовольняти відповідно диференціальні рівняння
Бесселя, Фур’є та Лежандра для звичайних функцій
повинні задовольняти відповідно диференціальні рівняння
Бесселя, Фур’є та Лежандра для звичайних функцій
![]()
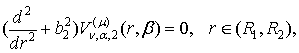 (15)
(15)
![]()
![]()
Фундаментальну систему розв’язків
для диференціального рівняння Бесселя ![]() складають функції
Бесселя першого роду
складають функції
Бесселя першого роду![]() та другого роду
та другого роду ![]() [3];
фундаментальну систему розв’язків для диференціального рівняння Фур’є
[3];
фундаментальну систему розв’язків для диференціального рівняння Фур’є 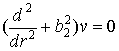 складають функції
складають функції ![]() та
та ![]() [2]; фундаментальну
систему розв’язків для диференціального рівняння Лежандра
[2]; фундаментальну
систему розв’язків для диференціального рівняння Лежандра ![]() складають узагальнені
приєднанні дійсні функції Лежандра першого роду
складають узагальнені
приєднанні дійсні функції Лежандра першого роду ![]() та другого роду
та другого роду ![]() [4];
[4];
![]()
Якщо
покласти
![]()
![]() (16)
(16)
![]()
то крайові умови (2) та умови спряження (3) для
визначення шести величин ![]() дають однорідну
алгебраїчну систему шести рівнянь:
дають однорідну
алгебраїчну систему шести рівнянь:
![]()
![]()
![]() (17)
(17)
![]()
Введемо
до розгляду функції:
![]()
![]()
![]()
Однорідна алгебраїчна система
(17) має ненульові розв’язки тоді й тільки тоді, коли визначник системи рівний
нулю [5]:
![]()
![]() (18)
(18)
У рівності (18) беруть участь
функції:
![]()
![]()
Алгебраїчне рівняння ![]() є трансцендентним
рівнянням для визначення власних чисел
є трансцендентним
рівнянням для визначення власних чисел ![]() ГДО
ГДО ![]() .
.
Підставимо в систему (17) ![]() й відкинемо останнє рівняння в силу лінійної залежності.
Якщо взяти
й відкинемо останнє рівняння в силу лінійної залежності.
Якщо взяти ![]() , де
, де ![]() підлягає визначенню,
то перше рівняння стає тотожністю, а два наступні рівняння утворюють
алгебраїчну систему двох рівнянь для
визначення величин
підлягає визначенню,
то перше рівняння стає тотожністю, а два наступні рівняння утворюють
алгебраїчну систему двох рівнянь для
визначення величин ![]()
![]() (19)
(19)
Згідно правил Крамера знаходимо, що
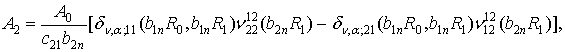
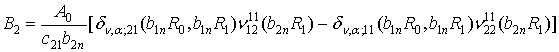 (20)
(20)
При відомих ![]() для визначення
для визначення ![]() маємо алгебраїчну систему двох
рівнянь:
маємо алгебраїчну систему двох
рівнянь:
![]() (21)
(21)
Визначник алгебраїчної системи (21) обчислюється
безпосередньо:![]()
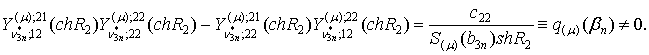 Алгебраїчна
система (21) має єдиний розв’язок [5]:
Алгебраїчна
система (21) має єдиний розв’язок [5]:
![]() (22)
(22)
![]()
Підставимо
визначені формулами (20) та (22)
величини ![]() у рівності (16). Одержимо
функції:
у рівності (16). Одержимо
функції:
![]()
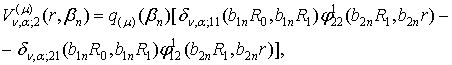 (23)
(23)
![]()
![]()
Згідно рівності (14) спектральна
вектор-функція ![]() стає
відомою (визначеною). При цьому її
норма визначається за звичайним правилом [5]:
стає
відомою (визначеною). При цьому її
норма визначається за звичайним правилом [5]:

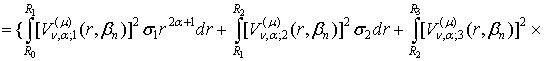
![]() (24)
(24)
Згідно
з роботою [7] сформулюємо твердження.
Теорема
1
(про дискретний спектр). Корені ![]() трансцендентного
рівняння
трансцендентного
рівняння ![]() складають дискретний
спектр ГДО
складають дискретний
спектр ГДО ![]() : дійсні, різні, симетрично розташовані відносно
: дійсні, різні, симетрично розташовані відносно ![]() й на півосі
й на півосі ![]() утворюють монотонну
зростаючу числову послідовність з єдиною граничною точкою згущення
утворюють монотонну
зростаючу числову послідовність з єдиною граничною точкою згущення ![]() .
.
Теорема
2
(про дискретну функцію). Система власних функцій ![]() ортогональна на множині
ортогональна на множині ![]() з ваговою функцією
з ваговою функцією ![]() , повна й замкнена.
, повна й замкнена.
Теорема
3
(про зображення рядом Фур’є). Будь-яка вектор-функція ![]() зображається за
системою
зображається за
системою ![]() абсолютно й
рівномірно збіжним на множині
абсолютно й
рівномірно збіжним на множині ![]() рядом Фур’є:
рядом Фур’є:
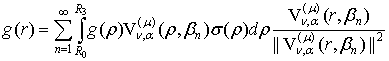 (25)
(25)
Ряд Фур’є (25) визначає пряме ![]() й обернене
й обернене ![]() скінченне гібридне інтегральне перетворення (СГІП), породжене на множині
скінченне гібридне інтегральне перетворення (СГІП), породжене на множині ![]() ГДО
ГДО ![]() :
:
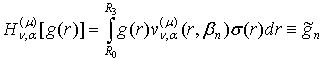 (26)
(26)
![]()
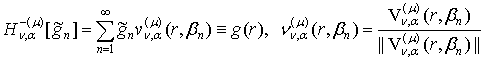 (27)
(27)
Визначимо
величини та функції:
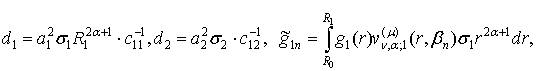
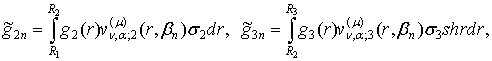
![]()
Теорема 4 (про основну тотожність). Якщо вектор-функція ![]() неперервна на множині
неперервна на множині
![]() , а функції
, а функції ![]() задовольняють крайові
умови
задовольняють крайові
умови
![]() (28)
(28)
та умови
спряження
![]() (29)
(29)
то має місце основна тотожність СГІП ГДО ![]() :
:
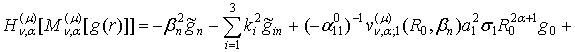
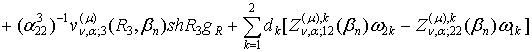 (30)
(30)
Доведення: Згідно правила (26) одержуємо:
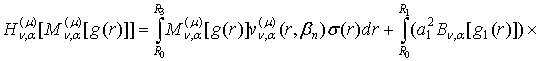
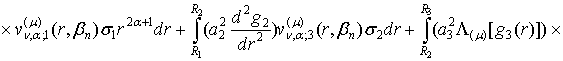
![]() (31)
(31)
Проінтегруємо в рівності (31) під знаками
інтегралів два рази частинами:
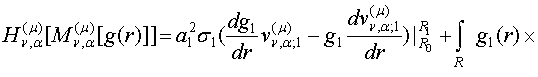
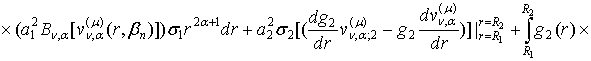
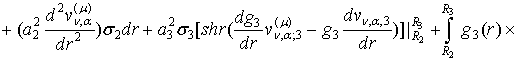
![]() (32)
(32)
Якщо ![]() , то знаходимо, що
, то знаходимо, що

![]()
![]() (33)
(33)
Якщо ![]() , то знаходимо, що
, то знаходимо, що

![]()
![]() (34)
(34)
В точці спряження ![]() маємо:
маємо:
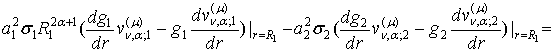
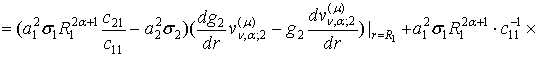
![]() (35)
(35)
тому, що в силу вибору чисел ![]() та
та ![]() вираз
вираз

В точці спряження ![]() маємо:
маємо:
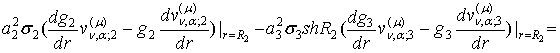
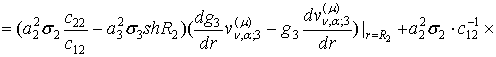
![]() (36)
(36)
тому, що в силу вибору чисел ![]() та
та ![]() вираз
вираз
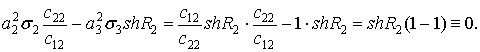
Із диференціальних тотожностей
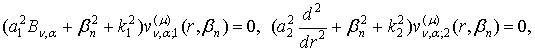
![]()
знаходимо диференціальні залежності

![]() (37)
(37)
Зауваження: При одержанні функціональних залежностей (35) та
(36) ми скористалися базовою тотожністю для випадку, коли умови спряження
неоднорідні (в правій частині (3) замість нуля стоїть ![]() ):
):
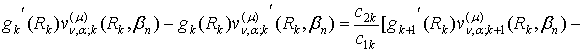
![]() (38)
(38)
Підставивши в рівність (32) функціональні
співвідношення (33)-(37), матимемо залежність:
![]()
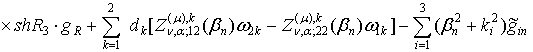 (39)
(39)
Оскільки
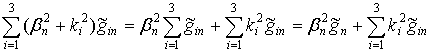 ,
,
то тотожність (39) співпадає з тотожністю (30).
Доведення теореми
завершено.
Висновок: Побудовані правила (26),
(27) та (30) складають математичний апарат для одержання інтегрального
зображення аналітичного розв’язку відповідних задач математичної фізики
кусково-однорідних середовищ.
Список
використаних джерел:
1.
Шилов Г.Е. Математический анализ.
Второй специальний курс. – М.: Наука, 1965. – 328с.
2.
Степанов В.В. Курс
дифференциальных уравнений. – М.: Физматгиз, 1959. – 468с.
3.
Ленюк М.П. Исследование
основных краевых задач для диссипативного волнового уравнения Бесселя. - Киев,
1983. – 62с. – (Препринт / АН УССР. Ин-т математики; 83.3).
4.
Конет І.М., Ленюк М.П. Інтегральні перетворення типу Мелера-Фока. – Чернівці: Прут, 2002. – 248с.
5.
Курош А.Г. Курс высшей алгебры. – М.:
Наука, 1971. – 432с.
6.
Ленюк М.П., Шинкарик М.І. Гібридні інтегральні
перетворення (Фур’є, Бесселя, Лежандра). Частина 1. – Тернопіль: Економічна думка,
2004. – 368с.
7.
Комаров Г.М., Ленюк М.П., Мороз В.В. Скінченні гібридні інтегральні
перетворення, породжені диференціальними рівняннями другого порядку. –
Чернівці: Прут, 2001. – 228с.