Игнатьева Н.К., Смирнов А.В.

Лесосибирский педагогический институт – филиал ФГАОУ ВПО «Сибирский федеральный университет», Лесосибирск

О роли геометрических построений в решении многовариантных задач

Многовариантные планиметрические задачи (задачи, содержащие в условии некоторую неопределенность), предлагаемые в структуре ЕГЭ с 2010 года (задание С4), доставляют немало хлопот как учащимся, так и обучающим. Причем трудности возникают как в сложных задачах, так и в самых простых, где намек на неоднозначность содержится в самой формулировке. Причины тому кроются не только в том, что у учеников недостаточно прочны знания о геометрических фактах или нет уверенного владения приемами решения планиметрических задач. Во многом успех в решении задач С4 зависит от того, насколько развита у школьников «многовариантная зоркость», позволяющая не потерять из виду ни одной из возможных конфигураций, соответствующих одному и тому же условию, но приводящих к различным решениям. Неоценимую помощь в развитии этого умения могут оказать задачи на построение.

В рамках данной статьи прежде всего важен последний этап решения задач на построение – исследование, который имеет целью выявить условия разрешимости задачи и определить число решений (т. е. фигур, удовлетворяющих условию задачи). Ведь именно при проведении исследования конструктивных задач можно научиться отвечать на вопросы, которыми предлагает заканчивать решение каждой задачи В. А. Далингер [2, с.4]:

– Можно ли построить другую фигуру, неравную найденной, но тоже удовлетворяющую условию задачи?

– При каких величинах заданных элементов нельзя построить заданную фигуру?

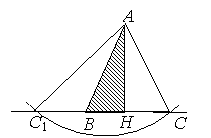Рассмотрим задачу 1 [1, № 351]. Построить треугольник, по двум сторонам и высоте, проведенной к третьей стороне. Пусть  – данные отрезки. Треугольник АВН определен по гипотенузе и катету (построение возможно при выполнении условия ). Для построения вершины С необходимо на прямой ВН построить точку, удаленную от А на расстояние b, т.е. найти точку пересечения прямой ВН и окружности ω (А; b).

На этапе исследования выясняем, что если , то таких точек две и при выполнении указанного выше условия  задача имеет два решения (треугольники АВС и АВС1). Если   и  или  и  ,то задача имеет одно решение (прямоугольный треугольник, в котором АС или АВ совпадает с АH). Если  или  или b=c=, то решений нет.

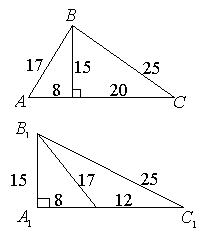251670528251669504251668480251674624251673600251672576251671552Это несложная задача на построение, в которой достаточно очевидны ответы на вопросы, связанные с многовариантностью. Именно с таких задач следует начинать пропедевтический этап обучения решению задач с неоднозначностью в условии; их решение может повысит вероятность того, что учащиеся научатся видеть всевозможные варианты расположения данных фигур. Например, предварительное решение задачи 1 поможет увидеть два случая при решении задачи 2 [3, с. 32]: Вычислить площадь треугольника, если две его стороны 25 и 17, а высота, проведенная к третьей стороне, равна 15. Не трудно заметить, что условия задачи определяют конфигурацию, рассмотренную в задаче 1 (при выполнении условий  и ), следовательно, можно сделать два чертежа для решения задачи. В первом случае , второй случай приводит к ответу 90.

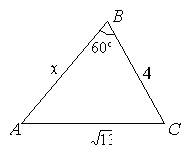Учащиеся, на наш взгляд, будут испытывать значительно меньше трудностей при решении задачи, если у них будет опыт работы с конфигурациями, похожими на те, которые получатся в результате построения чертежа к задаче. Рассмотрим решение задачи 3 [4, с. 40]: Найти сторону AB треугольника АВС, если АC = , BС = 4, АВС = 60.

0251671552251670528251669504По теореме косинусов . Данное уравнение приводится к квадратному  (1), имеющему два корня и . Привыкшие к тому, что задача чаще всего имеет одно решение, школьники пытаются найти некоторые условия, которым не удовлетворяет один из корней. Но проверка корней не дает оснований для отброса одного из них. Этих сомнений можно избежать, если предварительно решить задачу 4: Построить треугольник по двум сторонам (a и b) и углу против одной из них (β). Если начать построение с отрезка ВС, равного a, то решение задачи сведётся к построению точки А, которая лежит на луче, проведенном к ВС под данным углом β, и удаленной от точки С на расстояние b, т. е. принадлежащей окружности  ω (С; b).

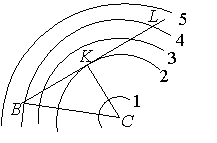При проведении исследования для острого угла имеем пять характерных случаев взаимного расположения луча и окружности, рассмотрение которых приводит к следующему выводу: задача имеет два решения если ; одно решение при  или ; и не имеет решения, если .

Предложенная в задаче 3 конфигурация удовлетворяет третьему случаю, т.е. задача имеет два решения и оба корня уравнения (1) удовлетворяют условию задачи.

Перебор всех вариантов – одна из составляющих решения многовариантной задачи, но с помощью геометрических построений их число можно сократить. Например, это можно увидеть при решении задачи 5 [3, с. 22]: Треугольник  АВС вписан в окружность радиуса 12. Известно, что АВ = 6,  ВС = 4. Найти АС. Согласно классификации, предложенной А. Г. Коряновым и А. А. Прокофьевым [3, с. 1] мы должны рассмотреть два 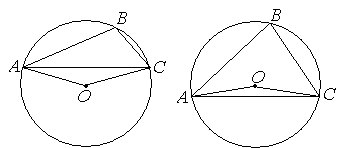251676672251672576251671552251670528251669504251675648251674624251673600случая: 1) точки О и В лежат по одну сторону от АС и 2) точки О и В лежат по разные стороны от АС. Однако числовые данные таковы, 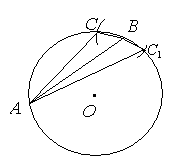251673600251672576251671552251670528251669504что случай, когда точки О и В лежат по разные стороны от АС, невозможен, что легко выясняется при непосредственном построении предложенной в задаче конфигурации, и для решения задачи достаточно рассмотреть только первый случай.

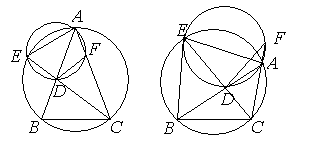251673600251672576251671552251670528251669504251678720251674624251677696Отметим полезность геометрических построений и при проведении последнего этапа решения задачи – проверке и исследованию полученного результата. При решении вычислительных задач большинство ответов можно проверить, просто проведя соответствующее построение. Оно же позволит во многих случаях заметить несоответствие между полученным результатом и рассматриваемой конфигурацией, там, где оно достаточно неочевидно. Для примера рассмотрим решение задачи 6: Продолжение биссектрисы CD неравнобедренного треугольника ABC пересекает окружность, описанную около этого треугольника, в точке E. Окружность, описанная около треугольника ADE, пересекает прямую AC в точке F, отличной от A. Найдите радиус окружности, описанной около треугольника ABC, если AC = 8, AF = 3,    BAC = 45. В данной задаче положение точек А, С и F не определено однозначно и возможны два случая: 1) точка F лежит между А и С; 2) точка А лежит между F и С. Рассмотрим первый случай. Используя свойства смежных и вписанных в окружность углов, имеем  поэтому треугольники СDF и CDB равны. Значит, ВС = AC – AF = 5. Тогда искомый радиус равен . Во втором случае решение аналогично, но ВС = 11 и радиус равен .

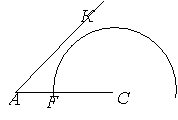0251670528251669504 В приведенном решении очень сложно увидеть невозможность первой конфигурации, однако если попробовать (для самоконтроля) выполнить построение циркулем и линейкой, то мы увидим, что при значении ВС = 5 треугольник АВС построить нельзя (действительно, расстояние от точки С до луча АК больше радиуса окружности).

Таким образом, систематическое решение задач на построение помогает учащимся научиться видеть неоднозначность в условии, сократить количество рассматриваемых случаев на этапе анализа, проверить правильность решения непосредственным построением и выявить случаи, когда найденные решения не определяют конфигураций, соответствующих начальным условиям задачи.

Литературы

1)                Атанасян Л.С. и др. Геометрия. 7 – 9 классы : учеб. для общеобразоват. учреждений / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. —  20-е изд. – М.: Просвещение, 2010. 384 с.

2)                Далингер В. А. Многовариантные задачи по планиметрии // Математика в школе. – 2011. – №6. – С. 3 - 8 .

3)                Корянов А. Г., Прокофьев А. А. Планиметрические задачи с неоднозначностью в условии (многовариантные задачи) // http://www.alexlarin.narod.ru: - URL: http://www.alexlarin.narod.ru/ege/2011/ C4-2011.pdf.

4)                 Рабинович Е. М. Задачи и упражнения на готовых чертежах. 7 – 9 классы. Геометрия. – М.: ИЛЕКСА, 2007. 60с.