Математика / 4. Прикладная математика
*Мотайло А.П.,
Хомченко А.Н.
*Херсонський національний технічний університет,
Чорноморський державний
університет імені Петра Могили, Україна
Порівняльний аналіз базисів октаедра
Постановка проблеми. Задача поліноміальної
інтерполяції функцій трьох незалежних змінних методом скінченних елементів, як
правило, розв’язується із залученням лінійних базисних функцій тетраедра та
трилінійних базисних функцій гексаедра. Просторові решітки із комірками у формі
гексаедрів, на відміну від тетраедральних, є наочними, але гірше
пристосовуються до границь області складної геометричної форми. При цьому
подрібнення решітки з тетраедрів, необхідне для досягнення певної точності
результату, обмежене розмірами тригранних кутів тетраедрів та потребує великого
об’єму розрахунків. У пошуку алгоритмів, ефективних за часом та об’ємом
обчислень, деякі спеціалісти МСЕ експериментують із розбиттям 3D-областей, пропонуючи
нові конфігурації просторових решіток, зокрема, із комірками у формі октаедрів.
Аналіз попередніх публікацій, ціль статті. Із появою октаедра у
якості скінченого елемента [1, 2] задача інтерполяції у 3D була вирішена для
центрованої моделі октаедра (7 вузлів) за допомогою поліноміальних функцій:
кусково-лінійних [1] та квадратичних [2]. Нецентрована модель октаедра
(6 вузлів) стала об’єктом досліджень авторів даної статті. У результаті
застосування різних способів побудови базисних функцій авторами статті були
отримані поліноміальні базиси першого та другого порядків, а саме, кусково-лінійний,
квадратичний та трилінійний базиси [3, 4] для нецентрованої моделі, та
тригонометричні базиси [5] для моделей октаедра з 6 та 7 вузлами. Наявність
різних систем базисних функцій на октаедрі, обумовлена неоднозначністю
розв’язку задачі інтерполювання функцій у 3D на цьому носієві, природно
потребує вирішення питання про ефективність використання певного базису
октаедра. При вивченні властивостей базисних функцій октаедра [1-5] в даній
роботі перевага надається їх інтерполяційним якостям.
Ціль статті – порівняти різні базиси октаедра на основі локальних
характеристик у вигляді визначника матриці Грама та числа обумовленості матриці
Грама.
Основна частина. У роботах [1-5] розглядається октаедр, вписаний у
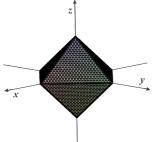
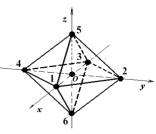
сферу одиничного радіусу. Прямокутну систему координат Oxyz обрано таким чином, що осі проходять через протилежні
вершини багатогранника, а початок системи координат співпадає з барицентром
октаедра (рис.1).
|
|
|
Базиси
7-вузлової моделі октаедра представлені в табл.1 функціями, що відповідають
вузлам 1, 3, та центральною функцією |
|
Рис.1. Моделі октаедра: а) центрована; б) нецентрована |
||
Решта базисних функцій легко отримати
з ![]() та
та ![]() циклічною
перестановкою координат.
циклічною
перестановкою координат.
Таблиця 1
Приклади базисних функцій
7-вузлової моделі октаедра
|
Базис октаедра |
Базисні функції |
|
Кусково-лінійний [1] |
|
|
Квадратичний [2] |
|
|
Тригонометричний [5] |
|
Таблиця
2
Приклади базисних функцій
6-вузлової моделі октаедра
|
Базис октаедра |
Базисні функції |
|
Кусково-лінійний [3] |
|
|
Квадратичний [3] |
|
|
Трилінійний [4] |
|
|
Тригонометричний [5] |
|
Аналізуючи
алгебраїчну структуру базисних функцій октаедра, легко помітити, що
поліноміальні базиси [1–4], за винятком квадратичного базису центрованої
моделі, є гармонічними по Лапласу. Як відомо [6], саме ця властивість покращує
апроксимаційні можливості базисних функцій при розв’язанні крайової задачі для
диференціального рівняння Лапласа.
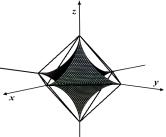
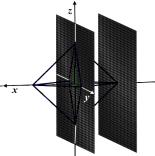
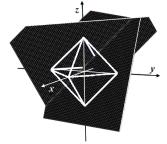
Геометрично
базиси [1–5] будемо
асоціювати із відповідними поверхнями нульового рівня базисних функцій ![]() та
та ![]() , представленими в табл. 3, 4.
, представленими в табл. 3, 4.
Таблиця
3
Поверхні нульового рівня
функцій ![]() та
та ![]()
базисів октаедра (7
вузлів)
|
Поверхні нульового
рівня базисної функції |
||
|
Кусково-лінійний [1] |
Квадратичний [2] |
Тригонометричний [5] |
|
|
|
|
|
Поверхні нульового
рівня базисної функції |
||
|
Кусково-лінійний [1] |
Квадратичний [2] |
Тригонометричний [5] |
|
|
|
|
Таблиця
4
Поверхні нульового рівня
функції ![]() базисів
октаедра (6 вузлів)
базисів
октаедра (6 вузлів)
|
Поверхні нульового
рівня базисної функції |
|
|
Кусково-лінійний [3] |
Квадратичний [3] |
|
|
|
|
Трилінійний [4] |
Тригонометричний [5] |
|
|
|
Обчислення
локальних характеристик кожного з базисів октаедра, а саме, величини визначника
матриці Грама та числа обумовленості матриці Грама в ![]() -нормі показало, що найкращими інтерполяційними
властивостями наділений тригонометричний базис 6-вузлової моделі [5], оскільки
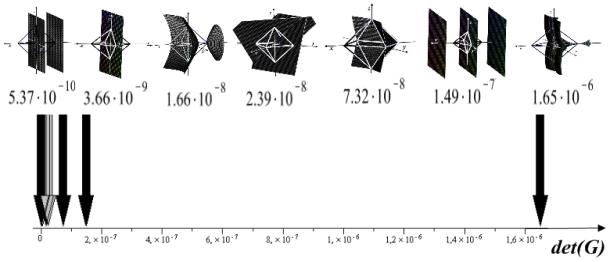
йому відповідає найбільше значення визначника матриці Грама. Наочно результати
обчислень демонструє рис.2.
-нормі показало, що найкращими інтерполяційними
властивостями наділений тригонометричний базис 6-вузлової моделі [5], оскільки
йому відповідає найбільше значення визначника матриці Грама. Наочно результати
обчислень демонструє рис.2.
|
|
|
Рис.2. Величина визначника матриці Грама для базисів октаедра [1–5] |
|
|
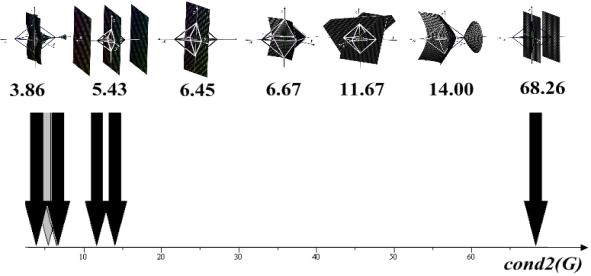
При цьому
матриці Грама всіх базисів октаедра є добре обумовленими, про що свідчить
величина числа обумовленості матриці Грама в ![]() -нормі (рис.3). На думку авторів [7] саме ця
характеристика є індикатором якості інтерполяції із залученням відповідного
базису, причому найкращим вважається той базис, число обумовленості матриці
Грама якого ближче до одиниці. В цьому сенсі перевага на боці тригонометричних
та кусково-лінійних базисів октаедра.
-нормі (рис.3). На думку авторів [7] саме ця
характеристика є індикатором якості інтерполяції із залученням відповідного
базису, причому найкращим вважається той базис, число обумовленості матриці
Грама якого ближче до одиниці. В цьому сенсі перевага на боці тригонометричних
та кусково-лінійних базисів октаедра.
|
|
|
Рис.3. Число обумовленості в |
Таким чином,
узагальнюючи результати вивчення локальних характеристик, можна вважати, що
кусково-лінійний базис нецентрованої моделі октаедра [3] наділений найкращими
інтерполяційними якостями в порівнянні з рештою представлених базисів октаедра.
За показниками числа обумовленості матриці Грама йому дещо програють
трилінійний та квадратичний базиси 6-вузлового октаедра [3, 4].
Висновки. В роботі проведений порівняльний
аналіз відомих базисів октаедра на основі локальних характеристик у вигляді
величини визначника матриці Грама та числа обумовленості цієї матриці. Отримані
характеристики для різних базисів октаедра свідчать про позитивний прогноз
інтерполяційних якостей базисів нецентрованої моделі. Найкращими
характеристиками при цьому наділений кусково-лінійний базис 6-вузлового
октаедра. Для визначення практичної цінності отриманих результатів дослідження
автори планують скласти бібліотеку тестових задач на скінченному елементі у
формі октаедра.
Література:
1. Greiner G. Hierarchical tetrahedral-octahedral subdivision for volume visualization / G.
Greiner, R. Grosso // The Visual Computer. – 2000. – І. 16. – Р. 357–369.
2. Bruijn H. Numerical Method for 3D Ideal Flow
[Електронний ресурс] / Han de Bruijn – Режим доступу: http://hdebruijn.soo.dto.tudelft.nl/jaar2010/octaeder.pdf
3.
Мотайло А.П. Базисы
шестиузлового октаэдра [Електронний ресурс]
/ А.П. Мотайло. – Материалы международной научно-практической конференции
"Перспективные научные исследования – 2011". Серия: Математика:
Прикладная математика (17–25 февраля
2011г.). – София, Болгария. – Режим доступу: http://www.rusnauka.com.
4. Тулученко Г.Я. Трилінійний гармонічний базис
октаедра / Г.Я. Тулученко, А.Н. Хомченко, А.П. Мотайло // Вестник Херсонского
национального технического университета. – Вып.3(42). – Херсон: ХНТУ, 2011. –
С. 424–429.
5. Мотайло А.П. Об октаэдре с тригонометрическим
базисом [Електронний ресурс] / А.П. Мотайло, А.Н. Хомченко // Материалы VII Международной научно-практической
конференции "Образование и наука без границ". Серия: Математика:
Прикладная математика (7–15 декабря 2011 г.). – Пшемысль, Польша: Sp.
z o.o. "Nauka
I studia", 2011. – Т. 27. Математика. Современные
информационные технологии – С. 25–29. – Режим доступу: http://www.rusnauka.com/Page_ru.htm.
6. Юлдашев О.И. Гармонические базисные функции для конечных элементов высокого порядка
аппроксимации [Електронний ресурс] / О.И. Юлдашев, М.Б. Юлдашева //
Объединенный институт ядерных исследований. Лаборатория информационных
технологий. Научный отчет 2006-2007. – Дубна: Объединенный
институт ядерных исследований, 2007. – С. 317–320. –
Режим доступу: http://lit.jinr.ru/Reports/SC_report_06-07/pdfall/p317.pdf.
7. Пинежанинов Ф. Свойства базисных функций [Електронний
ресурс] / Ф.Пинежанинов,
П.Пинежанинов // Exponenta.ru – Режим доступу:
http:// www.nsu.ru/matlab/Exponenta
RU/soft/Mathemat/pinega/a2/a2.asp.htm.
 а)
а)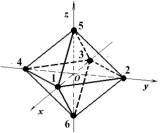 б)
б)