Педагогические науки/5.Современные методы преподавания

Э.З.Жарлыгасова

Костанайский государственный университет имени А.Байтурсынова, г.Костанай

Профессионально-ориентированные задачи в обучении математике студентов инженерных специальностей

Для овладения профессиональными знаниями студентам нужна серьезная подготовка по естественнонаучным дисциплинам, включающая в качестве непременного компонента математическую подготовку.

В настоящее время уровень развития науки и техники предъявляет к будущим специалистам, использующим в своей профессиональной деятельности математику, высокие требования к знаниям, умениям и навыкам математического, так и прикладного характера. Начиная с 60-х годов, параллельно идее политехнизации обучения обозначился процесс, связанный с рождением так называемой «прикладной направленности» в преподавании математики.

Теоретическая математическая подготовка не означает, что знания являются активным запасом студентов. Следует добиваться того, чтобы студенты были способны применять полученные знания в различных ситуациях. Такая способность может быть сформирована в процессе обучения, ориентированного на широкое раскрытие связей математики с общетехническими и специальными дисциплинами.

Одним из средств реализации межпредметных связей математики с общетехническими и специальными дисциплинами является обучение решению профессионально-ориентированных задач. В настоящее время особенно актуальным стало теоретическое обоснование методики использования задач в процессе обучения математике.

Решение задачи — это важнейший вид учебной деятельности обучающихся математике. В процессе решения задач усваивается математическая теория, развивается мыслительная деятельность, формируется личность обучаемого.

В большинстве исследований не прослеживается четкое разделение понятий профессиональной и прикладной направленности. Как правило, использован термин «прикладная направленность», в то время как зачастую при этом имеют в виду профессиональную направленность.

Однако до сих пор курс математики в большей своей части изолирован от технических дисциплин. Это изоляция настолько глубока, что студенты не видят в реальной ситуации известные им математические объекты, следовательно, не в состоянии пользоваться математическим аппаратом для описания этой ситуации. На практических занятиях задачи прикладного характера решаются редко, в связи, с чем навыки выпускников в решении таких задач оказываются не сформированными.

Как было указано ранее, одним из важных направлений осуществления прикладной и профессиональной направленности математической подготовки будущего инженера является отбор и изучение профессионально-ориентированных задач. Такое обучение может быть успешным при условии целостного подхода в организации этого процесса. Необходимо на всех этапах учебного взаимодействия через профессионально-ориентированные задачи эффективно использовать изучаемый математический аппарат, показывать его применение при изучении общетехнических дисциплин в будущей профессиональной деятельности инженера.

Пониманию будущими инженерами математики способствует решение задач методом математического моделирования. Между математикой и окружающей нас действительностью должно существовать какое-то связующее звено - специфический тип модели, с одной стороны, способной содержать информацию о том или ином предмете исследования, а с другой стороны, формулированной с помощью стандартных математических понятий и, стало быть, пригодной для применения мощного математического аппарата. Это и есть математическая модель исследуемого явления, служащая своего рода переводом закономерностей, выявленных конкретной наукой, на строгий математический язык. Построение математической модели исследуемого процесса включает в себя следующие этапы: 1) объект исследования; 2) функции состояния системы; 3) независимые переменные; 4) система координат; 5)причины эволюции системы; 6) причинно – следственная связь; 7) входные параметры системы; 8) условия применимости математической модели; 9) выходные параметры системы.

Рассмотрим движение баллистической ракеты, запущенной под углом к горизонту. Движение тела не будет прямолинейным, поскольку на него оказывает влияние не только сила тяготения, направленная вниз, но и сила тяги , действующая под некоторым углом к горизонту . Положение ракеты будем характеризоваться горизонтальной координатой и вертикальной координатой . Точка старта ракеты выбирается в качестве начала координат. Тогда функции выражает расстояние от проекции точки, в которой находится ракета в данный момент времени, на горизонтальную плоскость (поверхность земли), до начала координат, а функция определяет высоту ракеты над землей. Для вывода уравнений движения необходимо записать второй закон Ньютона в векторной форме. В горизонтальном направлении будет действовать горизонтальная составляющая силы тяги, а вертикальном – вертикальная составляющая силы тяги и вес Р. Согласно второму закону Ньютона ускорение тела в горизонтальном и вертикальном направлении будут пропорциональны соответствующим силам. В результате получаем следующую систему уравнений движения:

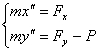
Составляющие силы тяги вычисляются по формулам , где - угол между направлением силы тяги и горизонтальной осью координат. Тем самым уравнения движения принимают вид , где .

Сила тяги действует до тех пор, пока все топливо не сгорит. Время сгорания топлива считается известным. Тогда справедливо равенство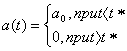, где - отношение силы тяги к массе ракеты , являющееся параметром процесса.

Предположим, что в начальный момент времени ракета находится в начале координат и покоится, что соответствует начальным условиям

Движение ракеты продолжается вплоть до некоторого момента времени Т, в который она приземлится, а значит, будем иметь нулевую вертикальную координату. Тем самым приходим к условию , из которого следует найти время приземления Т.

Параметрами рассматриваемой математической модели являются угол , вообще говоря, зависящей от времени, отношение и время сгорания топлива . рассматриваемая математическая модель имеет смысл лишь в том случае, когда ее начальное вертикальное ускорение положительно. Начальное ускорение в вертикальном направлении равно . Таким образом, приходим к следующему условию применимости модели

Таким образом, систематическое и целенаправленное использование профессионально-ориентированных задач в обучении математике на основе технологии наглядного моделирования технических процессов и реальных явлений в ходе ресурсного взаимодействия учебных дисциплин, ведет к повышению мотивации изучения математики на фоне активизации профессиональных знаний и качество предметных знаний, умений и навыков у студентов инженерных специальностей вузов.