Сичікова Я.О.

Бердянський державний педагогічний університет

Будова подвійного електричного шару на межі розділу напівпровідник-електроліт

         При зануренні напівпровідника в електроліт термодинамічна рівновага досягається за рахунок протікання на межі розділу різних електронних та іонних обмінних процесів. Електричні заряди протилежного знаку – електрони і дірки в напівпровіднику і іони в електроліті – будуть скупчуватися по обидва боки межі розділу, створюючи електричне поле. Виникає деяка різниця потенціалів, звана Гальвані-потенціалом – компенсуюча різниця хімічних потенціалів двох контактуючих фаз.

         Подвійний електричний шар на кордоні розділу напівпровідник-електроліт складається з трьох областей: області просторового заряду напівпровідника, шару Гельмгольца і області просторового заряду електроліту (рис. 1) [1].

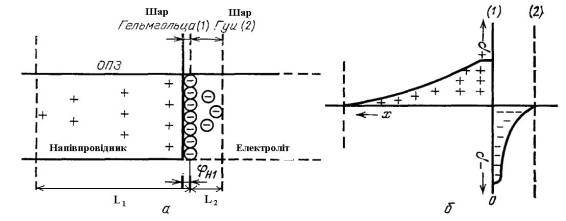
Рис 1. Схема структури подвійного електричного шару границі розділу напівпровідник-електроліт (ГРНЕ)

Гальвані-потенціал φ_1,2, тобто стрибок потенціалу між електронейтральними об’ємами напівпровідника (фаза 1) і електроліту (фаза 2), в загальному випадку повинен складатися з трьох доданків [1, 2]:

φ _1,2 = φ₁ + φ_o + ψ,

      де φ₁, φ_o, і ψ - падіння потенціалу відповідно в області просторового заряду напівпровідника (L₁ – товщина цього шару), в щільному шарі Гельмгольца товщиною d_o і шарі Гуї товщиною L₂ відповідно.

       Для поверхні напівпровідника n-типу, що безпосередньо контактує з електролітом, дебаєвська довжина L₁, що визначає товщину області просторового заряду дорівнює:

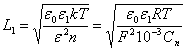
де ε_o - абсолютна діелектрична проникність, ε_o = 8,85 ⋅ 10^-12 Ф/м;

ε₁ - відносна діелектрична проникність напівпровідника, ε₁=9,61;

R - газова постійна, R = 8.314 Дж / (моль ⋅ К);

F - постійна Фарадея, F = eNa = 9.648 ⋅ 10⁴ Кл/моль;

n - число електронів в 1 см³ напівпровідника;

С_n - концентрація електронів, С_n = 10³ n / N_A моль/л;

N_A - число Авогадро, N_A = 6.022 ⋅ 10²³ моль ^-1.

Падіння потенціалу в ОПЗ визначається:

φ₁ = ξ₁ ∙ L₁,

де ξ₁ - напруженість електричного поля області просторового заряду.

Товщина шару Гуї L₂ описується аналогічним рівнянням:

,

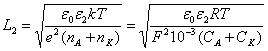Де ε₂ - діелектрична проникність електроліту;

  n_A і n_k - число аніонів і катіонів електроліті відповідно, см^-3;

С_A і С_K - концентрація аніонів і катіонів відповідно, моль / л;

Падіння потенціалу в шарі Гуі визначається наступним виразом:

ψ = ξ₂ ⋅ L₂

де ξ₂ - напруженість електричного поля в шарі Гуі.

У шарі Гельмгольца електричне поле постійне, як в плоскому конденсаторі з відстанню d_o між пластинами. У цьому разі потенціалу φ_o складає:

Для оцінки відносного падіння потенціалу в шарі Гельмгольца у напівпровіднику та електроліті можна скористатися наступними співвідношеннями [3]:

ϕ₁ / ϕ_o = L₁ε / (d_oε₁),

ϕ₁ / ψ = L₁ε₂ / (L₂ε₁).

Для напівпровідника n-типу з концентрацією електронів 2,3 х10¹⁸см^-3, який знаходиться в контакті з 25% розчином HF, падіння потенціалу в області просторового заряду напівпровідника повинно бути приблизно в 250 разів більшим, ніж у шарі Гельмгольца та в 230 разів більшим, ніж у шарі Гуі [4]. Таким чином, основна частина Гальвані-потенціалу падає в області просторового заряду напівпровідника.

Література

1. Батенков В.А. Электрохимия полупроводников: учеб. пособие / В.А. Батенков. – [2-е изд., допол.], – Барнаул: Изд-во Алт. ун-та, 2002. – 162 с.

2. Хомченко Г.П. Окислительно-восстановительные реакции / Г.П. Хомченко К.И. Севастьянова. – К.: Просвещение, 1989. – 141 с.

3. Дамаскин Б.Б. Химия / Б.Б.Дамаскин, О.А.Петрий, Г.А.Цирли — М.: Колос С, 2006. —672 с.

4. Плэмбек Дж. Электрохимические методы анализа / Дж. Плэмбек. – М.: Мир, 1985. — 496 c.