Строительство и архитектура / 7. Водоснабжение и канализация

К.т.н. Калякин А.М., Чеснокова Е.В., Сауткина Т.Н.

Саратовский государственный технический университет

имени Гагарина Ю.А., Россия

Модель процесса размыва перед препятствием типа мостовой опоры

До сих пор существует значительное количество нерешенных задач турбулентных течений жидкости в сложных граничных условиях (все эти задачи, как правило, касаются трехмерного обтекания границ). Существует несколько методов решения таких задач и одним из них, более близким к практически результатам, является создание упрощенной физической модели для каждого конкретного случая.

Часто бывает трудно заранее судить об однозначности модели, которая создается, прежде всего, на основании здравого смысла и результатов опытов; ввиду этого правильность основных ее выводов должна подкрепляться выполнением основных законов сохранения и, самое главное, она должна предсказывать явления в качественном и количественном отношениях.

Принимая во внимание сложность кинематики и динамики течения непосредственного перед препятствием в потоке со сдвигом, рассмотрим физику этого явления, придерживаясь лишь правдоподобных предположений и некоторых очевидных соотношений. В последующем рассматривается простейший случай незатопленного обтекания прямого кругового цилиндра плоским потоком со сдвигом.

В большинстве моделей используется аналогия с обтеканием кругового цилиндра потенциальным потоком; очертания линий тока в плоскостях, параллельных дну на некоторых расстояниях перед цилиндрами подобны линиям тока при обтекании цилиндра потенциальным потоком. Используется цилиндрическая система координат, в которой компоненты скорости обозначаются как

Очевидно, что поток, приближаясь к цилиндру, испытывает торможение (торможение в большей степени очевидно для осевого сечения) – так как известно, что именно на передней части цилиндра распределение давления при обтекании его вязким потоком почти совпадает с распределением давления при обтекании его потенциальным потоком идеальной жидкости [1]. Грубую оценку распределения давления возможно получить из формул для потенциального обтекания цилиндра [2].

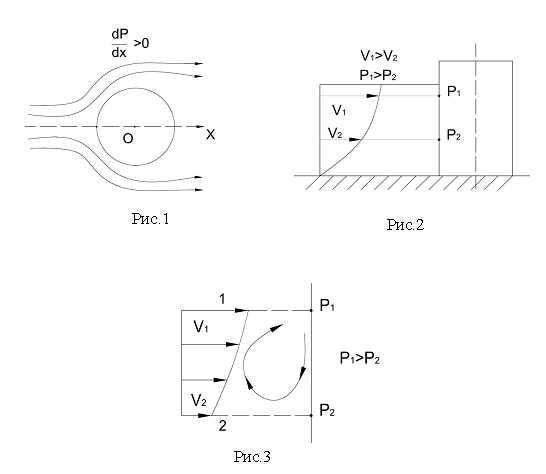
При приближении к цилиндру происходит замедление потока и кинетическая энергия его уменьшается – за счет этого повышается давление при приближении к передней критической точке О, (рис. 1).

Таким образом, в некоторой области перед цилиндром (во всяком случае – на осевой плоскости) будет существовать положительный градиент давления.

В потоке вязкой жидкости существует неравномерность распределения скоростей по глубине (графически она выражается эпюрой распределения скорости) – поэтому по причине преобразования кинетической энергии в потенциальную давление на поверхности цилиндра будет больше там, где больше скорость, т.е. возникает градиент давления по глубине, (рис.2). Возможно предположить, что именно последние две особенности обтекания являются причинами сложных вторичных течений перед препятствием. Так как вблизи осевого сечения давление на большем расстоянии от дна больше, чем на меньшем, то возникает в этой области течение, направленное от точки с давлением к точке с давлением , (рис. 3). Это течение тем интенсивнее, чем больше различаются скорости на горизонталях 1 и 2 (в частности в потоке без сдвига оно не будет существовать вообще). Это течение не может быть устойчивым, т.е. проходить сверху вниз по всей передней поверхности цилиндра. Давление, например, на горизонтали 2 у самой поверхности больше, чем на некотором расстоянии от нее, поэтому происходит закрутка линии тока и образуется вихрь [3].

Литература:

1. Милн-Томсон Л.М. Теоретическая гидродинамика. М.: Мир,1964, 655с.

2. Сергель О.С. Прикладная гидрогазодинамика/ О.С. Сергель. М.: Машиностроение,1971. 374с.

3. Высоцкий Л.И., Калякин А.М. Кречин С.Г. О методике и результатах исследований кинематики перед цилиндром, установленным нормально к дну в открытом потоке //Гидравлика сооружений и русловые процессы: Межвуз. темат. сб. Калинин: Калининский политехн. ин-т, 1982. С. 139-143.