Наблюдатель движения летательного аппарата (ЛА) в классе двухпараметрического структурно-устойчивого отображения

Универсальным методом исследования устойчивости динамической системы является второй метод А.М.Ляпунова. В качестве инструмента исследования, в которых используются некоторые специальные функции, называются функциями Ляпунова и базируются на двух теоремах А.М.Ляпунова.

На базе функций Ляпунова рассмотрена задача синтеза наблюдателя для искусственного спутника Земли с неопределенными параметрами (ИЗС) в классе двухпараметрического структурно-устойчивого отображения.

Использование метода анализа и синтеза наблюдателя в классе структурно-устойчивых отображений для искусственного спутника Земли (ИЗС), движения летательного аппарата (ЛА) показала устойчивости всех стационарных состояний.

Рассмотрим модель изолированного углового движения летательного аппарата (ЛА), которая в линеаризованном виде будет иметь следующий вид [14].

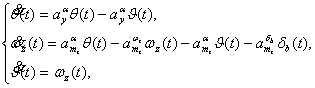
где - угол тангажа, - угол наклона, - угол атаки (), - угловая скорость, -сигнал управления рулем высоты, - соответственно коэффициенты угловой атаки, угловой скорости и сигнала управления.

Рассмотрим ЛА со следующими значениями параметров на некотором режиме полета [14,86]: . Считая входом системы отклонение рулей высоты, а выходом- угол тангажа, получим следующие матрицы:

, , .

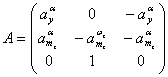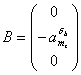Для удобства при проведении исследований запишем систему в векторно-матричной форме:

(1)

, , .

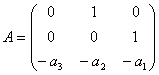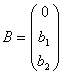Для системы (1) наблюдатель будет описываться следующим уравнением

(2)

Матрицу наблюдение выберем в классе двухпараметрических структурно-устойчивых отображений в виде:

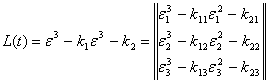(3)

Исследуем работу наблюдателя рассматривая ошибку оценивания . Для этого вычтем из (2) уравнение (3), учитывая введенную матрицу . Тогда получим следующее уравнение для ошибки

(4)

где источниками ошибки является начальное рассогласование

Исследуем поведение процесса . Система (3) обладает следующими стационарными состояниями:

(5)

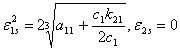(6)

Задаемся антиградиентом вектор функций Ляпунова по вектору скорости системы (4). Тогда компоненты вектора антиградиента будут равны:

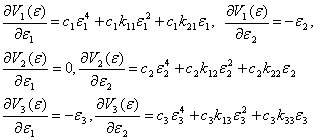
Находим полную производную по времени от вектор-функций Ляпунова с учетом уравнений состояний (4):

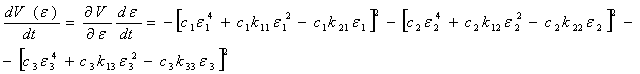Полное производное по времени от функций Ляпунова получим в виде знакоотрицательной функцией т.е. достаточное условие устойчивости выполняется.

Теперь по компонентам вектора градиента можем строить функцию Ляпунова.

Условие положительной определенности при на основе леммы Мороса получим в виде:

(7)

Получили условия робастной устойчивости стационарного состояния (5), в форме простейших неравенств (7).

Условия робастной устойчивости стационарного состояния (6) наблюдающего устройства (2) при

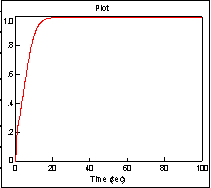
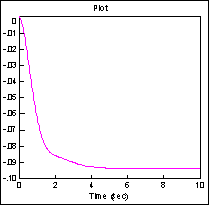
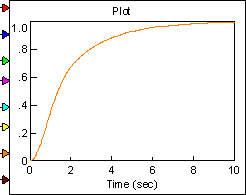
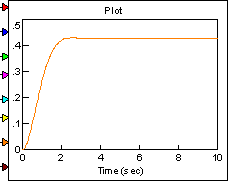
На рисунке 4.7 показана структурная схема системы (4.30), реализованная с помощью программного комплекса Vissim 6.0 на рисунках (4.8), (4.9), (4.10), (4.11) показаны графики катастрофа сборка.

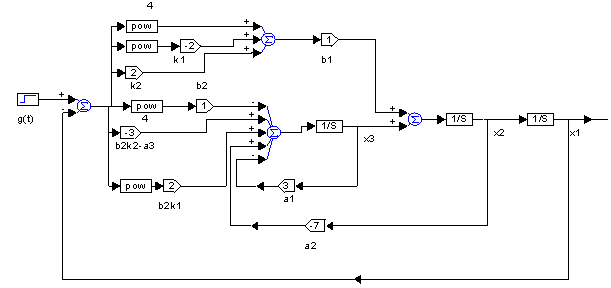
Рисунок 4.7

Рисунок 4.8

Рисунок 4.9

Рисунок 4.10

Рисунок 4.11

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Боднер В.А. Системы управления летательными аппаратами. М.: Машиностроение, 1973.-697с.

10 Заде Л., Дезоер Ч. Теория линейных систем. Метод пространства состяний. М.: Наука, 1970.-704с

.

2. Руш Н., Абетс П., Лалуа Н. Прямой метод Ляпунова в теории устойчивости. М.: Мир, 1980. 300с.

3. Бейсенби М.А., Турешбаев А.Т., Даутбаева А.О. Исследование наблюдающего устройства с повышенным потенциалом робастной устойчивости для одномерных систем методом функции А.М. Ляпунова.- Вестник КазНУ им. Аль-Фараби №4 2009.-52с.

4. Бейсенби М.А., Ержанов Б.А. Системы управления с повышенным потенциалом робастной устойчивости.-Астана 2002, -164с.