УДК 539.32: 622.023 Технические науки/ 2.Механика

Masanov Zh.K.¹, Azhihanov N.T, Turimbetov T.A.², Aimeshov Zh.A.³

¹Kazakh Academy of Transport and Communications named after M. Tinishbaev, Almaty, Republic of Kazakhstan.

²Caspian State University of Technologies and Engineering named after Sh.Eseno, Aktau, Kazakhstan.

³Internetional Kazakh-Turkish University named after H.A.Yassaui, Turkistan, Kazakhstan.

Mathematical modeling of diagonal fossils’, that have different forms, flexibly-movable condition in anisotropic environment

This article concerns with the numeral investigation of flexibly-movable intensity condition of double diagonal fossils that have been weakened with double periodic chinks.

We know about the researching works that deals with the modeling of the hole cleaning efficiency is an important criterion that should be well determined during drilling operations. The carrying capacity, the ability of transporting the drilled particles to surface, is one of the major roles of drilling fluids. Especially during underbalanced drilling operations in horizontal and deviated wells, flow behavior of the two-phase fluid should be well determined in order to improve the hole cleaning efficiency. Otherwise, an improper hole cleaning may result in differential pipe sticking, increased torque and drag and hence a severe economical loss.

They determined the slug interval by considering the slug frequency and the gas phase velocity. Then the flow pattern transitions were estimated from the slug intervals. They developed flow pattern maps for vertical air and water mixture through various noncircular conduits including concentric annuli. From these flow pattern maps, they concluded that the channel geometry has very little effect on the flow pattern transitions (1^st picture).

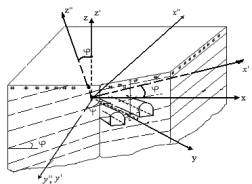
1^st picture. Drawing of area of the account

It was concluded that the flow patterns of cuttings are dependent on the total flow rate of the liquid and gas phase. It was also concluded that in order to avoid the formation of a stationary cuttings bed, an approximate boundary of minimum flow rate of each phase can be determined. The minimum requirements for gas and liquid flow rates were found to be always in the intermittent flow regime.

(1)

1^st picture. Environment weakened by two-period beams

The carrying capacity of the aerated drilling fluid was evaluated by using two-phase flow properties and a cuttings transport model. Moreover, a computer program was developed for the prediction of flow patterns, circulating pressures, optimum two-phase flow requirements, bit hydraulics and hole cleaning. It was concluded that dispersed bubble flow did not develop in the drill string and the annulus, and that the multiphase models calculated lower bottom hole pressures compared to dispersed model.

,

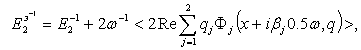(2)

Here < > - the sign of medium meanings; anisotropic settings;

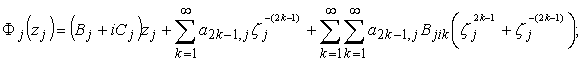
, , (3)

Transporting alevrolics ( ) is a equivalent of whole alevrolic flexibility modules and anisotropic settings that has been estimated in a connection of chink.

During the progress of the mathematical model, experimental data acquired from multiphase flow loop is integrated. Flow pattern and pressure loss estimations are compared with the experimental data and hence the model’s performance is evaluated.

Moreover, empirical equations are proposed for friction factor Oxyz determination corresponding to each flow pattern individually and mutually as well.

(4)

- can be find out by coefficient of modeling flexibility.

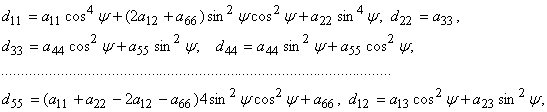(5)

(6)

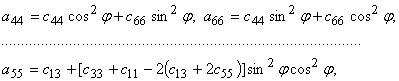
, , (7)

, ,

, ,

Similarly, the air compressor is used with a volumetric flow meter and an electropneumatic control valve to deliver required amount of gas into the loop. The compressed air mixed with the water before entering to the annular section. A pressure regulator is mounted before the gas flow meter as a safety measure and to keep the air pressure controlled prior to entering to the test section. The pressure of the gas phase is kept usually at 25 psi. The pressure of the loop, frictional pressure losses, liquid and gas flow rates are measured using the data acquisition system. Data logger and data acquisition software are used to gather and store the experimental data digitally. The determination of the locations of the pressure transmitters on the test section was one of the important tasks during setup design and construction. The data collected should be reliable since the mathematical model’s performance would be evaluated using the experimental data. Therefore,

entrance and exit effects are calculated for each casing-drillpipe configuration

using Equations 69 and 70. The entrance length is calculated by;

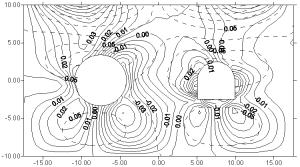
R₁=3,5M; R₂=2,5M; H=10M; L=5M; w/a=∞; H=10M;L=5M;y=45⁰; j=0; w/a=∞; - - w/a=3

y=90⁰; j=30⁰; w/a=6.0; - - w/a=2,5

For practical purposes, frictional pressure losses can be determined using friction factor correlations proposed separately for each flow pattern and flow properties of the mixture. A new mixture Reynolds number NRemixl based on liquid holdup term is introduced for intermittent flow.

When this wide range of application of two-phase flow in petroleum engineering is considered, the importance of the appropriate determination of flow parameters of two-phase fluid systems is remarkable. Several studies4-26 have been carried out for understanding the flow mechanism of two-phase fluid systems through pipe.

References

1. Ержанов Ж.С., Айталиев Ш.М., Масанов Ж.К. Устойчивость горизонтальных выработок в наклонно-слоистом массиве. Алма-Ата, Наука, 1971, 160с.

2. Ержанов Ж.С., Айталиев Ш.М., Масанов Ж.К. Сейсмонапряженное состояние подземных сооружений в анизотропном слоистом массиве. Алма-Ата: Наука, 1980 – 210с.

3. Масанов Ж.К., Атымтаева Л.Б., Жолдасова Ш.А., Жоламанова З.К. Упругая, упругопластическая состояние полостей в анизотропном массиве. / труды 1–го Центральноазиатского геотехнического симпозиума "Геотехнические проблемы строительства, архитектуры и геоэкологии на рубеже 21–го века"7 Астана, 2000. Том–1, –с. 240–2427