KURBANALIYEV L. T.
Candidate of the Physical and Mathematical Sciences,
Yassawi International Kazakh-Turkish University
DUYSENOVA G. A.
Master-Lecturer,
Yassawi International Kazakh-Turkish University
USE
OF THE MATRIX METHOD IN PROBLEMS OF DISTRIBUTION OF ELASTIC WAVES IN LAYERED
ENVIRONMENTS
A number of new results
of waves concerning distributions allows to gain a matrix method in layered
environments [1]. In particular, it was succeeded to prove that the medium with final number of the periods in the field of low
frequencies of W can be replaced is
transversal a homogeneous environment. The error of this replacement appears
generally proportional W2/n. In the elastic periodic environment this fact was proved earlier on the
basis of a number of hypotheses [2]. The specified approach is applied to more
difficult periodic environments in which between periodic packs of layers there
is a contact, with slipping of record of fluctuations the lands received by
means of seismographs, contain information as about the nature of the seismic
source which has generated this movement, and about properties of the
environment through which indignation (fig. 1) extended.
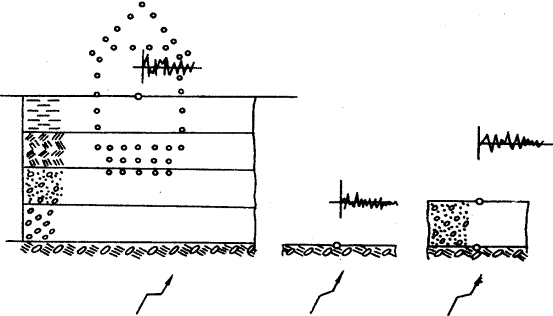
Figure 1. Schematic image of a task
Great practical value
is represented by settlement methods which at a stage of preliminary estimates
and final could give the necessary values of own frequencies of fluctuation of
soil, quantitative amendments at the expense of soil conditions.
The analysis of the matrixes
describing layers at distribution of elastic waves, gives the chance to write
down at small curvature of layers approximate expression [1]:
![]()
for a matrix of any poorly bent elastic layer in
which two-dimensional waves extend. Here k - the wave number, a matrix of C0 describes a plane-parallel layer, and r1 and r2 -
radiuses of curvature of borders respectively in the direction of distribution
of waves and along a layer, perpendicular to the first direction. The second in
the third members is characterized by amendments on curvature of a surface of
layers, correction matrixes ΔC1 and ΔC2 represent in
the form of meeting ranks on degrees of the relation of thickness of a layer to
length of a wave and have final ideas.
Let's consider distribution of flat
harmonious waves in the environment consisting of n - layers with
plane-parallel limits of the section (fig. 2), including each layer porous,
containing one of fillers: viscous liquid, gazo-liquid mix, gas.
Let's consider two
cases when the studied layered environment is concluded: (A) - between two
half-spaces (with indexes m=0 and m = m+1) or (B) - between a free surface and a half-space.
The task consists in
definition for a case (A) - amplitude and phase ranges, reflection and refraction
coefficients for all set hades; (B) - amplitude-frequency
phase ranges of horizontal and vertical shifts on a free surface and reflection
coefficients from a package of layers. These characteristics are necessary and
serve as the main sizes for definition of an increment of a ballnost of the
territory. Let's assume that from the bottom half-space (Z£Î) the flat harmonious wave with W
frequency at an angle θ and with
a phase speed of C from a remote source falls.

Boundary statements of the problem
between layers (in all points of a platform of contact) we set for both cases
in the form of equalities: speeds of shifts of a skeleton, tension firm
components, pressure of liquid and preservation of a stream of substances.
Figure 2. Models of environments
and direction of vectors
![]()
![]()
![]()
on the lower bound these conditions look like:
 (2)
(2)
Besides, on the upper
bound of the environment for a task (A) the condition (1), and for a case is
fair (B) conditions on a free surface in
shape have to be set:
![]() (3)
(3)
Decision method. Potentials and in a formula (3) taking into account the reflected and
refracted waves can be presented in the form of [2]:
 (4)
(4)
where ![]() and
and ![]() - potentials
of the reflected longitudinal and cross waves;
- potentials
of the reflected longitudinal and cross waves; ![]() and
and ![]() - potentials of the
longitudinal and cross refracted waves.
- potentials of the
longitudinal and cross refracted waves.
The solution of the
equation (4) meeting boundary conditions (1-3) we will write down so:
 (5)
(5)
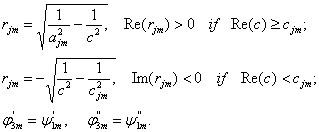
In expression (5) coefficients
are complex, depending on frequency. Their return values it is representable in
a look:
![]()
At the solution of seismological
tasks it is supposed [2]:

Tension and pressure in any
layer can be expressed through the generalized potentials:
![]()
![]() (6)
(6)

Further we will substitute (5)
in (4) and passing from shifts to speeds taking into account (6), we will
receive a ratio in a look:
![]()
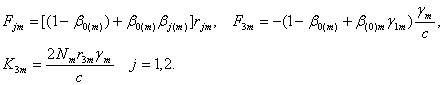
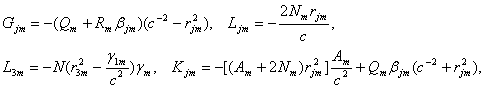
![]()
 (7)
(7)
Let's place the beginning of
coordinates on border between m-l and m layers (fig. 1), then speeds of shifts
and tension on this border will be connected with potentials of these layers
dependences:
![]() (8)
(8)
Speed of shifts and t tension –
a layer is expressed through potentials in a layer in a look:
![]()
![]() (9)
(9)
Let's exclude from (8) and (9)
potentials, we will receive a formula connecting speeds of shifts and tension
on the top and bottom borders of m a
layer:
![]()
![]() (10)
(10)
Using boundary conditions, we
will find ratios for m and layer m-1:
![]()
![]()
Repeating mathematical
transformations of n of times of this sort, we will receive communication
between characteristics of the bottom and top environment in a look:
![]()
![]() (11)
(11)
Substituting in (11) instead of
speeds of shifts and tension of their expression through potentials, in case of
a task (A) we will have:
 (12)
(12)
In the top half-space there are
no reflected waves therefore ratios are fair ![]() . In case of
falling of longitudinal waves of the first type on the lower bound of the
environment has to be
. In case of
falling of longitudinal waves of the first type on the lower bound of the
environment has to be ![]() . Let's
assume that
. Let's
assume that ![]() , then for
the second type of longitudinal and cross waves expressions are fair:
, then for
the second type of longitudinal and cross waves expressions are fair:
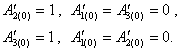
Considering above stated, ratios
(12) we can write down in shape:
 (13)
(13)
where ![]() - matrix elements
- matrix elements ![]()
For a task (B) system of the
equations (12) looks like:
 (14)
(14)
After some mathematical
transformations taking into account falling of each type of waves we will
receive:
 (15)
(15)
where ![]() - matrix elements
- matrix elements ![]()
Actions over matrixes
C, E and the solution of the equations (13) and (15) are carried out by means
of the COMPUTER. Coefficients of the reflected and refracted waves are defined
as the relation of amplitudes of the corresponding waves.
LITERATURE
1. Molotkov L.A. Matrix method in the theory of distribution of waves in layered elastic
and liquid environments. - L.: Science, 1984.
2. Thomson
W.T. Transmission of elastic waves trough a strati-fief solid material. J.
Appl. Phys., 1950, 21, N2, 89-93.