магистр Ахажанов С.Б., Макенова Л.С.
Карагандинский государственный университет имени
Е.А.Букетова, Казахстан
Изгиб пластины с упругоподатливыми опираниями при
действии равномерно распределенной нагрузки.
Рассмотрим пластину прямоугольной формы в
декартовой системе координат (
). Где 
- размеры пластины в направлении координатных
осей.
Представим функцию прогибов пластины в
следующем виде [1]:
(1)
где
- безразмерная функция прогибов; 
- параметр прогиба; 
- цилиндрическая жесткость пластины; 
- равномерно распределенная нагрузка; 
- закон изменения модуля материала; 
- параметр деформации; 
- начальный модуль материала
пластины; 
- коэффициент Пуассона.
Внутренние усилия
пластины определяются по следующим формулам [1]:
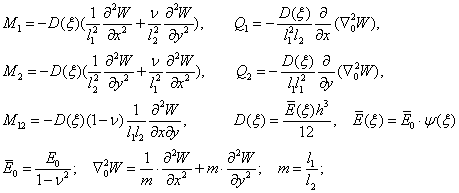(2)
Если пластина имеет упругоподатливые опирания,
то безразмерная функция прогибов 
и параметр прогиба 
приобретает следующий вид:
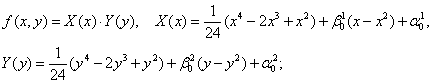(3)
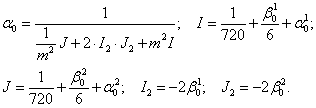(4)
Параметры упругоподатливого опирания 
принимают различные значения.
В частности имеем:
а) при жестком
защемлении: 
б) при шарнирном
опирании: 
В общем случае они
определяются по следующим формулам:
(5)
где 
- податливости упругих закреплений.
В качестве примера
рассмотрим пластину с упругоподатливыми опираниями в кооординатной системе (
),
загруженную равномерно распределенной нагрузкой интенсивностью 
.
Используя, выше
приведенные формулы (1), (2), (3), (4) находим прогиб и внутренние усилия
пластины.
Построим эпюры прогиба
и внутренних усилии пластины (рисунок 1)
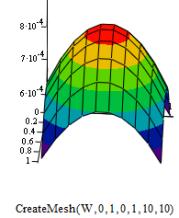
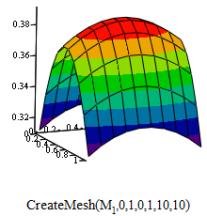
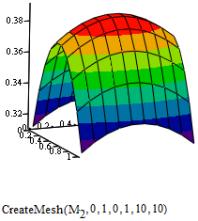
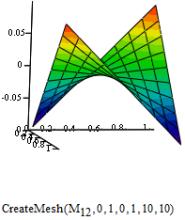
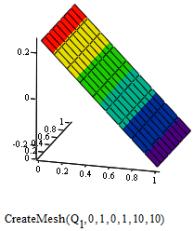
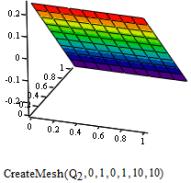
Рисунок
1. Прогиб, внутренние усилия (изгибающие моменты, поперечные силы и крутящий
момент) пластины.
Таким образом,
полученные результаты позволяют определить напряженно-деформированное состояние
пластины с упругоподатливыми опираниями.
Список
использованных источников
1 Турсунов К.А.
Механика мембран, пластин и оболочек. Караганда, 2009,С. 142.