Model of a temperature field
of preparation from a single thermal source at abrasive processing
Dyakonov A. A., Ermilov
S.A.
South-Ural State
University, Russia, Chelyabinsk
Only
thin layers of part blank are subject to sudden (impulsive) heat in the grinding
zone. That is why during description the temperature field the geometry of part
blank may be neglected, in other words for 3-D system it can be considered the
case of half-space heating by sources moving on the surface. As used here the
process of heat transmission mathematically comes to the second boundary
problem for heat conduction equation in the half-space. Integral Decision is known for
this linear model [1]:
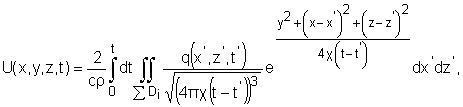 (1)
(1)
ñ— thermal diffusivity of material; ρ — density of
material; χ — thermal diffusivity of material; D i — the scope of i-sources — abrasive
grain in XZT- system limited by surface Ôi (x,z)=0 (fig. 1);
q — intensity of heat source.
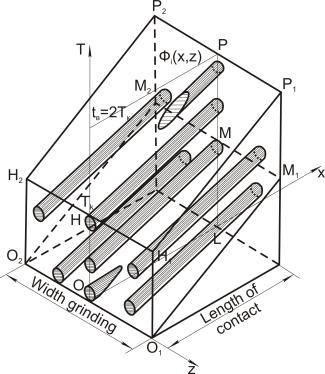
Fig. 1. The principle scheme of thermal sources influence
It is
rather complicated integral and not evaluated by famous special function.
As it
is researched by many investigators the theory of high-speed sources can be
used for grinding process offered by N.N. Ryikalin [2]. Using of this theory
allows decreasing the number of independent coordinates and reducing integral
equation for separately thermal source to following format:
 (2)
(2)
U(y,z,t) — the
temperature in the moment t at the
depth of y with z–coordinate in breadth; λ — thermal conductivity of material;
l ç — the length of abrasive grain blunting area.
Starting
from the purposes of the research it is important to consider the temperature
of thin layers of part blank to the moment of biting the next abrasive grain.
By S.N.
Korchak [3] researched that for definition impulsive temperature it is required
to consider thin layers of part blank within the limits of 0,05-0,002 mm as
this depth is marginally allowed for scraping off material by single abrasive
grain.
Alongside
with this, change of temperature at the depth part blank surface in the
following diapason 0,002–0,010 mm are negligible as temperature drastic
recession is observed at the depth of higher than 0,015 mm [3].
Because
of it y=0 and we can come to 2-D system. As the result dependence (2) come to
the following equation:
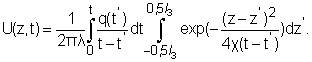 (3)
(3)
This
dependence (3) describes the heating process from single thermal source. For
realizing cooling-down calculation the dependence (3) computes with zero
intensity of heat source (4).
![]() (4)
(4)
Taking
into account expression (4) we have get the dependence describing cooling-down
from single heat source (5).
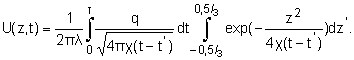 (5)
(5)
In the
result taking into account dependences (3—5) the temperature from single heat
source — abrasive grain — can be described by system of equations (6):
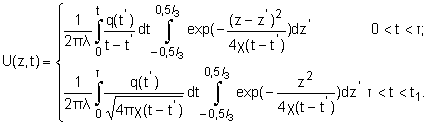 (6)
(6)
The
equation (6) describes the heating and cooling-down process cause of single
heat source — abrasive grain taking into account flank flow-out at circle breadth.
However,
using of this integral for calculations involves difficulties even by computer.
Analysis
of the literature concerning thermal physics of solids makes clear that integral
(3) can be expressed by special
functions: error function erf(x) and integral exponential function Ei:
·
error function erf(x):
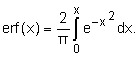 (7)
(7)
·
integral exponential function Ei:
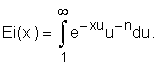 (8)
(8)
The meanings of
these functions are learned [4]. As the result we have get:
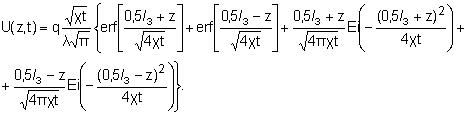 (9)
(9)
q — intensity of
heat source; λ — thermal conductivity of material; a — the half of length
heat source (a=0,51ç); erf(x) —error
function;Ei — integral exponential function, z — coordinate of source endwise
z, ҳ — thermal diffusivity of material.
Using
the method of reflected sources [4] to describe cooling-down process is used
equation for heating (9) from which analogue equation subtracted with τ:
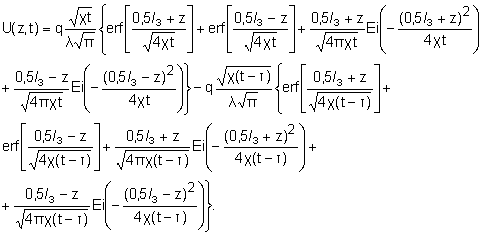 (10)
(10)
As the
result equation (6) can be signed by equations system (11):
![]()
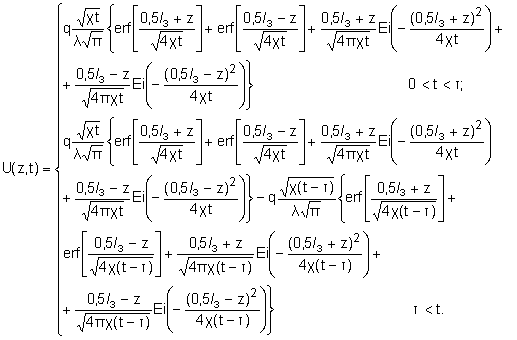
There are
no difficulties concerning calculation of equation system (11) both by computer
and by hand.
Conclusion
Consequently
received spatial model rather exactly describes impulsive temperature field of
part blank unit section. At that, adaptation of superposition method and
parallel displacement of coordinates allow to research the temperature field of
part blank by grinding in any required time moment of it formation. And also it
allow to research heat spreading both cutting velocity vector direction and
transversely to it.
References
1.
Reznikov A.N. The Physics of cutting.
M.: Mechanical engineering, 1979. 288 p.
2.
Ryikalin N.N. Account and modeling of a
temperature field of a product at grinding // The
bulletin of mechanical engineering. M.,
1963. ¹1. P.74–77.
3.
Korchak S.N. Productivity of process of
grinding of steel details. M.: Mechanical
engineering, 1974. 280 p.
4.
Karslou G. The Thermal conductivity. M.: Science, 1964. 488 p.