УДК 631.95
Канд. экон. наук Гришин
А.А., докт. техн. наук Гришин А.П.
транспирация растений
как диссипативный процесс с временной
фрактальной структурой
Введение
Процесс
транспирации – испарение воды с поверхности листа растения с целью его
охлаждения, является энергоинформационным процессом в физиологии растений. В
его основе лежит принцип энергетической экстремальности самоорганизации (ПЭЭС),
и закон выживания (ЗВ) сформулированный И.И. Свентицким и заключающийся в том,
что растение для своего развития и роста максимально использует свободную
доступную часть энергии солнечного излучения, называемой фотосинтезной
эксергией [1]. Скорость фотосинтеза
зависит от температуры поверхности листа и имеет максимальное значение при
определенной величине температуры, которая обеспечивается самоорганизующимся
термодинамическим процессом транспирации. На транспирацию у растений
расходуется до 95% всей потребляемой воды.
Основное назначение
транспирации заключается в снижении температуры листа растения – tл,
воспринимающего тепловую эксергию солнечного излучения (СИ) – Em, путем испарительного охлаждения и приближении её к
температурному оптимуму фотосинтеза – to, что в свою очередь направлено на достижение
максимальной продуктивности растений – урожая.
Этот процесс протекает в открытой нелинейной термодинамической системе –
устьичный аппарат растения, вода, окружающая среда с потоком тепловой солнечной
энергии, той её части, способной превращаться в другой вид энергии и называемой
тепловой эксергией.
Здесь и далее воспользуемся
положениями, определениями и терминологией используемой в [2,3,4].
Этот приток энергии к системе должен
обеспечить достижение системой критического
состояния (точки бифуркации) с последующим выходом из этого состояния скачком
по типу фазового перехода испарения.
Скачек характеризует
образование новой диссипативной
структуры. Диссипативные структуры –
это сложные пространственно-временные структуры, возникающие под действием
термодинамических сил в системе, находящейся далеко от термодинамического
равновесия и существующие только в режиме постоянной подпитки, в нашем случае
тепловой эксергии СИ.
Важнейшими
характеристиками диссипативных структур являются: время жизни, область локализации и фрактальная размерность.
Лист, а в некоторых случаях и все растение
в целом является открытой структурой, в которой имеется приток внешней энергии.
Другими словами процесс транспирации
можно отнести к диссипативным процессам, протекающим в нелинейной открытой термодинамической системе. Исследуем его на
фрактальность.
Объект
и методы исследований
Снижение температуры листа на величину
разности двух значений температур – ΔТо = tл -
to обеспечивает увеличение скорости фотосинтеза и с
одновременным попутным накоплением и расходованием во время испарения
дополнительной эксергии теплоты ΔеТ, которая и
обуславливает энергетический градиент транспирации.
Интегральный транспирационный расход за
некоторый период времени определяется выражением:
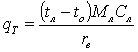 , (1)
, (1)
где Мл – общая масса листьев,
Сл
– удельная теплоемкость массы листьев, rв
– удельная теплота испарения воды [5].
Учитывая, что числитель выражения (1)
определяет теплоту регулируемого транспирацией нагрева листа с последующим
испарением воды, то этот процесс является неравновесным фазовым переходом в открытой
нелинейной динамической системе терморегулирования растения, которая получает
из внешней среды энергию в виде тепловой эксергии СИ, являющейся переменной
порядка самоорганизующегося процесса транспирации. При этом параметром
управления самоорганизующегося процесса транспирации будет расход транспирации
и параметры других сопутствующих процессов.
Таким образом, выражение для
самоорганизующегося процесса транспирации в виде взаимосвязи переменной порядка
и параметра управления можно записать в виде:
![]()
![]() . (2)
. (2)
Эта зависимость определит экстремальную
энергетическую целенаправленность самоорганизующегося процесса транспирации
согласно ПЭЭС.
Исследуем транспирацию с позиций
возможности отнести её к фрактальным структурам, и определим фрактальную
размерность структуры процесса, если он окажется таковым.
Фрактальность присуща большинству естественных структур, особенно живым
существам. Она также присутствует в процессах и явлениях, и в такой их
характеристике как время.
Первое свойство, самоподобие, оно означает, что
части в некотором роде связаны с целым. Это подобие может быть
"точным", как в треугольнике Серпинского, где каждый маленький
треугольник геометрически идентичен большому треугольнику. Такая точная форма
самоподобия существует только математически.
В действительности, самоподобие «качественно», то есть
объект или процесс являются подобными в различных масштабах, пространственных
или временных, статистически. Каждый масштаб напоминает другие масштабы, но не
идентичен им. Это свойство самоподобия делает фрактал масштабно-инвариантным.
Эта особенность масштабирования по степенному закону, которая объясняет
масштабную структуру, например, листа растения, оказывается вторым свойством
фракталов, фрактальной размерностью, которая может описывать либо
физическую структуру, либо временной ряд.
Основное свойство евклидовой
геометрии - это то, что размеры являются целыми числами. Линии одномерны.
Плоскости двумерны. Тела трехмерны.
Свернем из листа бумаги трубу. Она не является трехмерным,
потому что в ней есть отверстия. Она также не является двумерным, потому что
обладает внутренним пространством. Несмотря на то, что она находится в
трехмерном пространстве, она меньше чем тело, но больше чем плоскость. Её
размерность находится где-то между двойкой и тройкой. Это нецелое число и есть
фрактальная размерность.
Фрактальная размерность характеризует наполняемость
пространства и описывает структуру при фрактальном масштабировании. Для
физических фракталов такое преобразование имеет место в пространстве. Для
временного ряда масштаб изменяется во времени.
Традиционно, процессы во времени
рассматриваются либо как случайные, либо как детерминированные. Последние
определены с момента появления, поэтому в большинстве случаев отдается
предпочтение детерминистскому представлению о времени. Вместе с тем мы можем
наблюдать случайные отклонения от предопределенного течения процесса.
Самоорганизующиеся системы характеризуются случайностью и
детерминизмом, которые сосуществуют. Детерминизм дает нам закон природы.
Случайность привносит новшество и разнообразие. Саморазвивающаяся система - это
та, которая не только может пережить случайные удары, но также может поглотить
их, чтобы в соответствии с ЗВ оздоровить всю систему.
Рассмотрим пример из области фрактальных структур.
Фрактальные структуры созданные природой более устойчивы. Например, лист
растения имеет центральный стебель с ответвлениями, которые в свою очередь
продолжают ветвиться. В каждой группе ответвлений средний диаметр уменьшается
согласно степенной зависимости, причем так, что диаметр каждой группы зависит
от диаметров предыдущей группы. В каждой группе имеется диапазон диаметров,
который может быть описан только в вероятностном смысле.
То есть, имеется общий детерминизм, выраженный средними
диаметрами со степенной зависимостью от номера группы и внутригрупповая случайность, характеризуемая дисперсией
диаметров. Фрактальная структура, имеющая общий детерминизм и внутригрупповую
случайность более стабильна и устойчива к ошибкам, чем другие структуры,
поскольку при фрактальном масштабировании ошибка уменьшается вследствие
степенной зависимости и вероятностной структуры.
Далее приведем результаты исследований, касающиеся
фрактального характера процесса
транспирации, а точнее его временного ряда.
Результаты исследований и их
обсуждение
В.Н. Жолкевич отмечает, что
процесс транспирации имеет колебательный характер, с периодом в десятки секунд, в отличие от уже
известных суточных колебаний, что говорит о нелинейности и согласованности
протекания процесса транспирации в виде временного ряда.
В [6] он с соавторами приводит
его графическое изображение для листа Erythrina Variegata, рис. 1. Нами был
исследован этот временной ряд на его фрактальный характер. При помощи метода нормированного размаха или (R/S) анализа была определена фрактальная размерность ряда. Результаты
расчетов приведены в таблице 1.
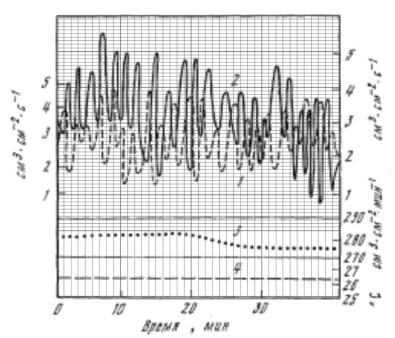
Рис. 1. Процесс транспирации листа Erythrina Variegata – 2,
поступления
воды в лист – 1, скорость воздуха – 3,
температура
воздуха – 4
Предварительно исходный
временной ряд с шагом длительностью 30 секунд был преобразован в ряд, состоящий
из логарифмических отношений каждого последующего значения к предыдущему, при
этом результирующий ряд становится короче на один шаг.
Далее весь ряд делим на лаги
длиной по 10, 20 и 40 шагов. Для каждого случая получаем соответственно 8, 4 и
2 лага. В каждом случае и для каждого лага находим матожидание – т,
стандартное отклонение – σ, минимальное значение – min, максимальное значение –
max, их
разность – размах – R, нормированный размах – R/S. Минимальные и максимальные значения
находим для преобразованного в виде кумулятивного (накопленного) ряда в
пределах каждого лага. Для каждого случая находим среднее значение
нормированного размаха, которое и будет значение функции при определении
показателя Херста.
Для многих
временных рядов наблюдаемый нормированный размах – отношение разности
максимального и минимального значения транспирации для заданного отрезка
времени (лага, n), R к стандартному отклонению, вычисленного для значений
транспирации того же лага, S хорошо описывается эмпирическим выражением:
![]() , (4)
, (4)
где c –
константа, Н – показатель Херста, который связан с фрактальной
размерностью D соотношением D = 2 – H.
Таблица 1. Расчет нормированного размаха
|
п |
№ |
т |
σ |
min |
max |
R |
R/S |
R/Sср |
|
10 |
1 |
1,01 |
0,27 |
-0,41 |
0,15 |
0,56 |
2,07 |
2,66 |
|
2 |
1,01 |
0,22 |
-0,08 |
0,35 |
0,43 |
1,97 |
||
|
3 |
1,08 |
0,30 |
-0,86 |
0,22 |
1,08 |
3,64 |
||
|
4 |
1,06 |
0,63 |
-0,80 |
0,91 |
1,71 |
2,70 |
||
|
5 |
1,20 |
0,65 |
0,00 |
1,75 |
1,75 |
2,68 |
||
|
6 |
0,97 |
0,31 |
-0,31 |
0,53 |
0,84 |
2,73 |
||
|
7 |
1,03 |
0,40 |
0,00 |
1,04 |
1,04 |
2,58 |
||
|
8 |
-1,09 |
4,57 |
-3,38 |
9,96 |
13,34 |
2,92 |
||
|
20 |
1 |
1,01 |
0,24 |
-0,41 |
0,35 |
0,76 |
3,17 |
3,92 |
|
2 |
1,07 |
0,48 |
-0,80 |
0,92 |
1,73 |
3,59 |
||
|
3 |
1,08 |
0,51 |
0,00 |
1,87 |
1,87 |
3,65 |
||
|
4 |
-0,03 |
3,34 |
-1,27 |
16,37 |
17,63 |
5,28 |
||
|
40 |
1 |
1,04 |
0,38 |
-1,16 |
0,87 |
2,02 |
5,38 |
6,90 |
|
2 |
0,53 |
2,43 |
-0,15 |
20,26 |
20,42 |
8,42 |
На рис.2 представлена графическая
зависимость, построенная для данных таблицы 1, а также её аппроксимирующее
выражение в виде степенной функции.
Фрактальная размерность
временного ряда дает оценку степени изломанности временного ряда, а также его
внутреннего характера. То есть прямая имеет фрактальную размерность 1, а
фрактальная размерность случайного временного ряда с нормальным распределением
составляет 1,5.
Фрактальная размерность временного ряда представляет собой
функцию изменения масштаба от периода времени. Она важна, потому что
подчеркивает, что процесс может находиться между детерминистическим характером
(линия с фрактальной размерностью 1) и случайным (фрактальная размерность
1,50). В общем случае фрактальная размерность ряда может находиться в пределах
от 1 до 2. Чем ближе размерность к двум, тем больше инверсий имеет случайная
последовательность. Чем ближе к единице, тем более предсказуемым становится
процесс.
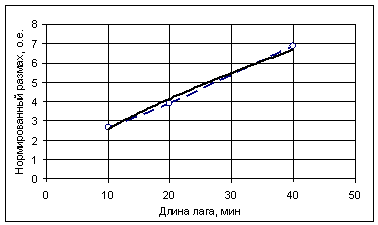
Рис. 2. Зависимость
нормированного размаха от длины лага – прерывистая линия и её аппроксимирующее выражение,
R/S = 0,53 n0,69
– сплошная линия. Достоверность аппроксимации R2 = 0,99
То есть по своему характеру он в большей степени подвержен
прогнозированию, поскольку обладает персистентностью – долговременной памятью о
структуре процесса.
Таким образом, при показателе Херста равном Н = 0,69 имеем фрактальную размерность D = 1,31, что подтверждает сосуществование
детерминизма и случайности во фрактальном временном ряде, описывающим процесс
транспирации как самоорганизующийся процесс, идущий согласно ЗВ и обладающий
долговременной памятью.
Выводы
1.
Процесс транспирации
имеет фрактальную структуру с размерностью D = 1,31, который является
неравновесным фазовым переходом испарения в открытой нелинейной
динамической диссипативной
системе терморегулирования растения с притоком внешней энергии в виде тепловой
эксергии солнечного излучения, которая является переменной порядка.
2.
При этом параметром
управления самоорганизующегося процесса транспирации будет расход транспирации
и параметры других сопутствующих процессов.
3.
Показатель
Херста Н=0,69, что подтверждает сосуществование детерминизма и
случайности во фрактальном временном ряде, описывающим процесс транспирации как
самоорганизующийся процесс, идущий согласно ЗВ и обладающий долговременной
памятью.
Литература:
1.
Свентицкий И.И. Энергосбережение в АПК и
энергетическая экстремальность самоорганизации. – М.: ГНУ ВИЭСХ 2007.
2.
Хакен Г.
Синергетика. – М.: Мир, 1980.
3.
Николис Г.,
Пригожин И. Познание сложного. Введение: Пер. с англ. – М.: Едиториал УРСС,
2003. – 344 с.
4.
Петерс Э.
Фрактальный анализ финансовых рынков. – М.: Интернет – трейдинг, 2004.
5.
Мудрик В.А., Свентицкий И.И.
Биоэнергетические аспекты оценки влагообеспеченности растений. Пущино, Пущинский центр биологических исследований АН
СССР, 1981.
6. Жолкевич В.Н., Гусев Н.А., Капля А.В. и др. Водный обмен растений. – М.:
Наука, 1989. – 256 с.