Д.т.н., проф. Пилькевич И.А., аспир. Маевский А.В.

Житомирский национальный агроэкологический университет, Украина

Математическая модель взаимодействия между популяциями

Решение современных экологических проблем имеет не только важное научное, но и общее значение для жизни человечества. Особую роль в этой связи играет изучение динамики развития экологических систем и их оптимального управления в интересах человечества. Отдельно следует выделить проблему взаимодействия между популяциями, которую изучает эволюционная экология.

В начале 20 века Лотка (1925 г.) и Вольтерр (1926 г.) при изучении взаимодействия между популяциями использовали сравнительно прочную, хотя и весьма упрощенную теоретическую основу [1]. Их уравнения конкуренции сильно повлияли на развитие современной экологической теории и представляют собой хороший пример математической модели важного экологического явления. Однако математическая модель Лотки-Вольтерра имеет ряд недостатков, поэтому в работе предложена усовершенствованная модель взаимодействия между популяциями, основанная на универсальной модели динамики популяций [2].

Рассмотрим общеизвестную модель Лотки-Вольтерра типа „хищник-жертва”, описывающую взаимодействие между популяциями [3]:

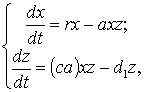
где – количество жертв;

– количество хищников;

– удельная скорость роста популяции жертв при небольшом числе хищников;

– эффективность хищника (удельная скорость, с которой хищник убивает жертву);

– эффективность преобразования хищниками биомассы жертв;

– удельный коэффициент смертности, с которой вымирают хищники при отсутствии жертвы.

В первом приближении эта модель адекватна. Однако, в реальной ситуации, эта модель не оправдывает себя, поскольку она слишком упрощена в связи с предположением, что количество жертв растет экспоненциально при отсутствии хищников, а это не соответствует действительности. В этом случае эффективность хищников можно заменить константой.

Модель Лотки-Вольтерра можно улучшить заменой экспоненциальной зависимости логистической. В результате этого получим модель Розенцвайга-МакАртура, которая больше всего соответствует реальной ситуации взаимодействия между популяциями [4]:

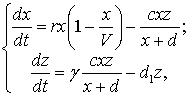
где – ёмкость экологической ниши.

Следует отметить, что в рассмотренных математических моделях динамики популяций не учтены следующие факторы: способность популяций к расселению; тенденция к захвату новых мест проживания; действие защитных механизмов, повышающих способность особей популяций к выживанию; способность выдерживать неблагоприятные условия существования. Кроме этого на колебания динамики численности популяций влияет миграция (иммиграция или эмиграция) особей и не всегда есть возможность пренебречь её показателями. Также четко не определено влияние таких факторов сопротивления окружающей среды, как: дефицит воды; нехватка пригодных мест обитания; неблагоприятные погодные условия и др.

Исходя из вышеизложенного, в работе предлагается усовершенствовать известную модель взаимодействия между популяциями типа „хищник-жертва” с учетом логистического роста путем введения обобщенной логистической модели динамики популяций, адекватность которой подтверждена в [5]. В результате получим систему дифференциальных уравнений:

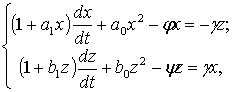
где и – соответственно скорость роста популяций жертвы и хищника;

, , , – параметры, характеризующие влияние сдерживающих факторов на развитие популяций;

– коэффициент взаимного влияния популяций.

На рис. 1 представлена динамика развития популяций хищника и жертвы, полученная при решении системы (5) с помощью системы компьютерной алгебры Mathcad.

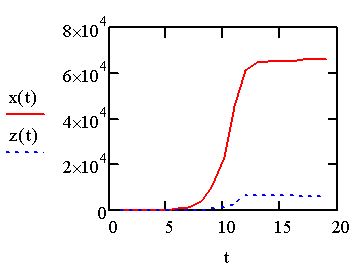
Рис. 1. Зависимость количества жертв и хищников от времени

Следует отметить, что по оси абсцисс отложено не реальное время (например, 2004…2012 года), а номера дискрет, по которым проводился расчет количества жертв и хищников. При этом года, анализируемые в работе, приходятся на 11-13 дискреты.

Таким образом, с целью учета основных факторов, влияющих на динамику развития популяций, известную модель взаимодействия между популяциями целесообразно усовершенствовать путем введения в её состав обобщенной логистической модели динамики популяций.

Литература:

1. Смит, Дж. Модели в экологии / Дж. Смит; пер. с англ. под. ред. и с предисл. А. Д. Базыкина. – М. : Мир, 1976. – 184 с.

2. Тимонін, Ю. Б. Універсальна модель систем: методологічний аспект / Ю. Б. Тимонін, Ю. Б. Бродський, І. Г. Грабар // Віс. ЖНАЕУ: наук.-теорет. зб. – 2009. – №1. – С. 358-366.

3. Богобоящий, В. В. Принципи моделювання та прогнозування в екології : підручник / В. В. Богобоящий, К. Р. Курбанов, В. М. Шмандій, П. Б. Палій. – К. : Центр навч. літ-ри, 2004. – 216 с.

4. Rosenzweig, M. L., MacArthur, R. H. (1963). Graphical representation and stability conditions of predator–prey interactions. American Naturalist 97: 209–223.

5. Пількевич, І. А. Оцінювання адекватності логістичних моделей динаміки популяцій копитних України / І. А. Пількевич, О. В. Маєвський, В. І. Котков // Збірник наукових праць Подільського державного аграрно-технічного університету. – Кам’янець-Подільський, 2011. – Спец. вип. до VI науково-практичної конференції „Сучасні проблеми збалансованого природокористування”, 24-25 лист. 2011 р. – С. 35–39.