Экономические науки/ 8. Математические методы в экономике

К.э.н., Смотрова Е.Е.

Волгоградский государственный аграрный университет, Россия

Эконометрическое моделирование производства мяса Волгоградского региона

Одной из главных задач прикладной экономики животноводства является прогнозирование с использованием массива статистических данных производства основных видов его продукции. [3]

Системы взаимосвязанных уравнений позволяют учесть структуру взаимосвязи между эндогенными и предопределенными переменными, к которым относят как экзогенные, так и лаговые эндогенные.

В общем случае система одновременных уравнений включает структурные уравнения вида:

Ax + By = ε

где х = (х₁,…, x_m)_t – экзогенные переменные;у = (у₁, .., у_l)_t – эндогенные переменные, а число уравнений системы в общем случае равно k.

Определение оценок элементов матриц Аи В требует использования специального математического аппарата. В случае, когда матрица В квадратная и неособенная, можно записать решение системы структурных уравнений, выразив их через экзогенные переменные:

у = –В^–1Ах+ В^–1ε

Так как экзогенные переменные не коррелированы с ошибками, то для каждого уравнения системы можно применить обычный метод наименьших квадратов, оценки параметров которого будут состоятельные, несмещенные и эффективные. Результатом этой операции будет матрица оценок В^–1А в соответствии с косвенным методом наименьших квадратов (КМНК). [1]

За последние 10 лет потребление основных видов продуктов в регионе еще далеко от рекомендуемых норм питания по молоку и мясу. При норме потребления мяса и мясопродуктов (включая субпродукты) 75 кг на душу населения в год фактически расходуется на эти цели только 48-73 кг; молока и молокопродуктов 197-201 кг (при норме 305 кг/год); соответствует рациональной норме только потребление яиц – свыше 250 млн. шт. в год. [4]

Для составления структурной эконометрической модели производства мяса с учетом его потребления были отобраны:

- эндогенные факторы: Y₁ – производство мяса в год, тысяч тонн; Y₂ – потребление мяса в год, тысяч тонн; Y₃ – цена производства 1 тонны мяса, рублей.

- экзогенные факторы: X₁ -поголовье КРС, тысяч голов; X₂ - приплод молодняка в расчете на 100 маток, телят; X₃ – площадь кормовых культур, тысяч га; X₄ - ввоз мяса и мясопродуктов, включая импорт в год, тысяч тонн; X₅ - цена производства 1 тонны зерна, рублей; X₆ - среднедушевые доходы населения в месяц, рублей.

Период исследования проводится с 2000-2012 гг.

Структурная модель годового производства мяса, его потребления, а также цены производства 1 тонны мяса, сформированная в виде трех взаимосвязанных уравнений, представлена на рисунке 1.

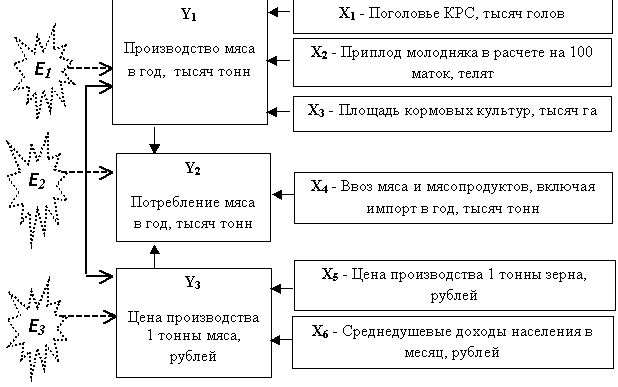
Рисунок 1 – Структурная схема системы эконометрических уравнений

Поскольку все уравнения системы сверхидентифицируемые, то для оценки структурных коэффициентов используем двухшаговый метод наименьших квадратов.

На первом этапе определим параметры каждого из приведенных уравнений в отдельности обычным МНК, используя программу MS Excel и ее встроенный модуль «Анализ данных – Регрессия».

;

;

.

На втором этапе, в исходных структурных уравнениях заменим эндогенные переменные, выступающие в качестве факторных признаков, их расчетными значениями:

Применяя обычный МНК к каждому из уравнений по отдельности полученной системы определим структурные параметры модели. Таким образом, система одновременных уравнений производства мяса в Волгоградской области представлена в Таблице 2.

Таблица 2 - Система эконометрических уравнений производства и потребления мяса с учетом цены его производства

Моделируемый показатель	Уравнение системы	R^2	F- кри-терий
Производство мяса, тыс. тонн	У1 = 92,2 + 0,00074у3 - 0,05x1 + 1,19 x2 + 0,06 x3, (44,5) (0,0001) (0,05) (0.456) (0,038)	0,974	36,4
Потребление мяса в год, тыс. тонн	У2 = -43,24 + 1,575у1 - 0,01у3 + 0,82 x4 , (114,5) (1,11) (0,001) (0,658)	0,913	15,0
Цена производства 1 тонны мяса, рублей	У3 = -76401,7 + 793,3у1 + 2,187x5 + 1,07 x6, (49394,8) (456,7) (2,15) (1,626)	0,979	72,3

Проверка значимости коэффициентов регрессии с помощью t – критерия Стьюдента показала недостаточную значимость параметров X, поэтому была построена альтернативная структурная эконометрическая модель следующего вида:

Таблица 2 – Альтернативная система эконометрических уравнений производства мяса с учетом цены его реализации

Моделируемый показатель	Уравнение системы	R^2	F- кри-терий
Производство мяса, тыс. тонн	У1 = 97,02 + 0,00069у3 + 0,0055x1 (15,12) (0,0001) (0,029)	0,939	37,7
Потребление мяса в год, тыс. тонн	У2 = -506,07 + 5,89у1 - 0,0082у3 + 4,432 x4 (204,8) (1,94) (0,0029) (1,55)	0,946	25,6
Цена производства 1 тонны мяса, рублей	У3 = -111642 + 1123,2у1 + 2,926x5 (23150,3) (215,5) (1,599)	0,969	75,9

Так, цена производителя и поголовье КРС оказывает положительное влияние на производство мяса в год. Увеличение стоимости производства мяса на 1 тыс. рублей в год приводит к сокращению потребления мяса на 0,0082 тыс. тонн. В свою очередь, увеличение цены производителя 1 тонны мяса на 2,926 рублей в год обусловлено увеличением стоимости 1 тонны зерна.

Верификация регрессионных уравнений проводилась с помощью средней ошибки аппроксимации, значения которой составили 3,01%, 3,13% и 11,74% соответственно, что указывает на высокие прогнозные свойства модели. Коэффициенты детерминации, равные 0,939 и 0,969 говорят, что 93,9% и 96,9% вариации производства мяса и его стоимость объясняется вариацией учтенных в соответствующих моделях факторов.

Таким образом, построенная системная модель развития животноводства учитывает рыночные взаимосвязи стоимости производства продукции, годового производства и потребления мяса и мясопродуктов от ряда натуральных и стоимостных показателей.

Поскольку оценка значимости уравнений регрессии с помощью F – критерия Фишера и t – критерия Стьюдента показали хорошие результаты, данная модель может быть использована для прогнозирования.

Необходимо отметить, что для повышения экономической эффективности развития отрасли животноводства в рамках ведомственной целевой программы «Развитие мясного скотоводства Волгоградской области на 2013-2015 годы» выделено 725776,8 тысяч рублей на увеличение поголовья КРС, численности работников, занятых в мясном скотоводстве и выручки от реализации скота мясных пород и их помесей.

В Волгоградской области министерством сельского хозяйства разработаны ведомственные целевые программы и порядки предоставления субсидий на возмещение части затрат на уплату процентов по кредитам и займам на развитие отрасли животноводства в целях повышения продовольственной безопасности региона.

Литература

1. Мазаева, Т.И. Структурное эконометрическое моделирование и обоснование прогнозирования развития животноводства (на материалах Волгоградской области): монография / Т.И. Мазаева, Е.Е. Смотрова. – Волгоград: ФГБОУ ВПО Волгоградский ГАУ, 2013. – 132 с.

2. Постановление Правительства Волгоградской обл. от 27.11.2012 N 538-п"Об утверждении долгосрочной областной целевой программы "Развитие сельского хозяйства и регулирование рынков сельскохозяйственной продукции, сырья и продовольствия на 2013 - 2020 годы" [Электронный ресурс] // www.consultant.ru.

3. Смотрова, Е.Е. Прогноз производства молока в Волгоградской области / Е.Е. Смотрова, Т.И. Мазаева // Экономика сельского хозяйства России. – 2009. № 11. – С. 68-73.

4. Смотрова, Е.Е. Животноводство региона в контексте продовольственной безопасности / Е.Е. Смотрова // Региональная экономика: теория и практика. 2013. № 6 (285). – С. 48-54.