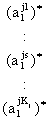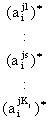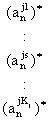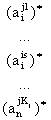Современные информационные технологии/ 2. Вычислительная техника и программирование

Илипов М.М., к.ф.-м.н. Искакова А.С.

Евразийский национальный университет им. Л.Н. Гумилева, Казахстан

Вывод предпочтения прецедента с вычислительным алгоритмом Минимакс в системе Matlab

Одними из характерных особенностей поставленных перед совершенствованием работы RFID являются составление и изучение алгоритма выбора прецедента при наблюдении ситуационного вектора с количественными координатами.

Ранее в работе Прохорова М. Д. и Федунова Б.Е. [1] был введен алгоритм выбора прецедента при наблюдении ситуационного вектора с количественными координатами.

Пусть состояние ПрС/С описывается ситуационным вектором с координатами (х_{1, …}, x_n) и каждая координата х_i - лингвистическая переменная с множеством термов прецедентам (блок прецедента). Каждая строка матрицы представляет собой конкретный ситуационный вектор, при котором в прошлом успешно реализовался соответствующий прецедент.

Перенумеруем строки блока прецедента d_j двумя индексами: первый индекс – номер прецедента (здесь он является номером блока), второй индекс – порядковый номер ситуационного вектора в этом блоке.

Представим алгоритм определения функции принадлежности m_dj (x₁, .. x_i, .. x_n) прецедента d_j, интерпретируемого как нечёткое множество на универсальном множестве. U_d = Ux₁ ´ … ´ Ux_i ´ … ´ Ux_n, где Ux_i - универсальное множество, на котором заданы термы лингвистической переменной x_i, а U_d – декартово произведение универсальных множеств Ux_i .

Рассмотрим принадлежности нечёткого множества, который образован следующим отношением Ú … Ú (x_i) Ú … Ú (x_n) , где через “Ú” обозначена операция “max”, или в терминах математической логики предикат конъюнкции.

Анализируя весь блок логических высказываний, относящийся к прецеденту d_j (блок соответствующих строк матрицы знаний), замечаем, что они представляют собой объединение соответствующих нечётких множеств, образовавшихся при рассмотрении строк выделенного блока. Функция принадлежности этого объединения, отождествляемая с функцией принадлежности прецедента d_j будет

= (Ú … Ú (x_n)) Ù… Ù (x₁) Ú … Ú (x_n))

где через «Ù» обозначена операция “min”, или в терминах математической логики предикат дизъюнкции.

Формально представленный алгоритм определения функции принадлежности прецедента d_j можно записать в виде:

а) фиксируем произвольную точку (,

б) для каждого блока матрицы знаний, соответствующего d_j, определяем m_dj (x₁, .. x_i, .. x_n) в этой точке согласно схеме таблицы 2.

Таблица 2.

№ п/п	Координаты ситуационного вектора					max	min	d
	x1		xi		xn
:	:	:	:	:	:	:	:	:
:	:	…	:	…	:	…	…	:

На основе текущих измерений точка формируется с количественными значениями его координат. Только в этой фиксированной точке в момент поступления замера и нужно определить значение функции принадлежности m_dj (x₁, .. x_i, .. x_n).

При наблюдении ситуационного вектора [1] с количественными координатами (все координаты вектора измерены по числовым шкалам) для выбора наиболее подходящего прецедента вовсе нет необходимости полностью определять функции принадлежности m_dj(x₁, .. x_i, .. x_n) на всем множестве точек универсального множества. Достаточно рассчитать их значение только для фиксированных числовых значений координат вектора, который мы получили в результате наблюдения. В результате для каждого прецедента d_j мы получим число d_j, являющееся степенью принадлежности d_j точке .

Исходя из такой интерпретации, наиболее предпочтительным прецедентом будет прецедент , для которого = d_j.

Программа предназначеная для выбора прецедента по методу Минимакс при наблюдении ситуационного вектора с количественными координатами в системе Matlab представлена на рисунках 1-2.

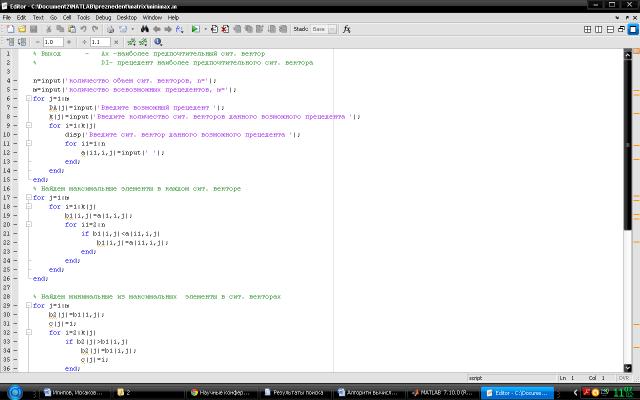
Рисунок 1. Программа для выбора прецедента по методу Минимакс при наблюдении ситуационного вектора с количественными координатами в системе Matlab.

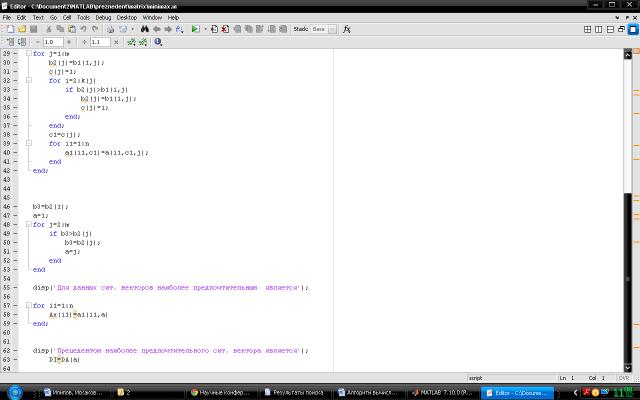
Рисунок 2. Продолжение программы для выбора прецедента по методу Минимакс при наблюдении ситуационного вектора с количественными координатами в системе Matlab

Литература:

1. Прохоров М. Д. Федунов Б.Е. Вывод по прецеденту в базах знаний бортовых интеллектуальных систем, размещаемых на борту антропоцентрических объектов.

2. Дшхунян В.Л. Электронная идентификация. Бесконтактные электронные идентификаторы и смарт-карты / В.Л. Дшхунян, В.Ф. Шаньгин. – М.: ООО «Издательство АСТ»: Издательство «НТ Пресс», 2004. – 695 с.