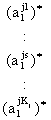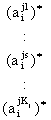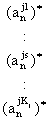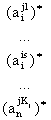Современные информационные технологии/ 2. Вычислительная техника и программирование

Илипов М.М., к.ф.-м.н. Искакова А.С.

Евразийский национальный университет им. Л.Н. Гумилева, Казахстан

Алгоритм максимин выбора прецедента в помехоустойчивости системы RFID

Систему работы RFID можно представить как процесс, посредством которого собираются данные в определенный момент времени. Причем не редко встречаются ситуации, когда в определенный момент времени одновременно поступают данные от n меток, случайным образом перекрывающих друг друга.

Прежде всего, представим алгоритм определения функции принадлежности m_dj (x₁, .. x_i, .. x_n) прецедента d_j, интерпретируемого как нечёткое множество на универсальном множестве. U_d = Ux₁ ´ … ´ Ux_n, где Ux_i - универсальное множество, на котором заданы термы лингвистической переменной x_i, а U_d – декартово произведение универсальных множеств Ux_i .

Анализируя весь блок логических высказываний, относящийся к прецеденту d_j (блок соответствующих строк матрицы знаний), замечаем, что они представляют собой объединение соответствующих нечётких множеств, образовавшихся при рассмотрении строк выделенного блока. Функция принадлежности этого объединения, отождествляемая с функцией принадлежности прецедента d_j будет

= (Ù… Ù (x_n)) Ú… Ú (x₁) Ù … Ù (x_n))

где через «Ú» обозначена операция “max”, или в терминах математической логики предикат дизъюнкции.

Формально представленный алгоритм определения функции принадлежности прецедента d_j можно записать в виде:

а) фиксируем произвольную точку (,

б) для каждого блока матрицы знаний, соответствующего d_j, определяем m_dj (x₁, .. x_i, .. x_n) в этой точке согласно схеме таблицы 1.

Таблица 1.

№ п/п	Координаты ситуационного вектора					min	max	d
	x1		xi		xn
:	:	:	:	:	:	:	:	:
:	:	…	:	…	:	…	…	:

На основе текущих измерений точка формируется с количественными значениями его координат. Только в этой фиксированной точке в момент поступления замера и нужно определить значение функции принадлежности m_dj (x₁, .. x_i, .. x_n).

При наблюдении ситуационного вектора [1] с количественными координатами (все координаты вектора измерены по числовым шкалам) для выбора наиболее подходящего прецедента вовсе нет необходимости полностью определять функции принадлежности m_dj(x₁, .. x_i, .. x_n) на всем множестве точек универсального множества. Достаточно рассчитать их значение только для фиксированных числовых значений координат вектора, который мы получили в результате наблюдения. В результате для каждого прецедента d_j мы получим число d_j, являющееся степенью принадлежности d_j точке .

Исходя из такой интерпретации, наиболее предпочтительным прецедентом будет прецедент , для которого = d_j.

Систему работы RFID можно представить как процесс, посредством которого собираются данные в определенный момент времени. Причем не редко встречаются ситуации, когда в определенный момент времени одновременно поступают данные от n меток (см.[2]), случайным образом перекрывающих друг друга.

Согласно работ [2, 9-10], поведенческая модель радиоприемного тракта (RX chain) состоит из Verilog-модулей, которые реализуют процессы детектирования поднесущей, фильтрации, усиления и детектирования входного высокочастотного сигнала, представленного в языке Verilog 16-разрядным двоичным сигналом. Иными словами, из работ [1, 8-9] следует, что сигнал по форме является вектором х объема 16, связанных с влиянием перекрывающих сигналов. То есть на искажение влияют n перекрывающихся сигналов. Допустим, что истинный сигнал представим в виде вектора l₀, на который наложили искажение u, состоящее их n сигналов (векторов), принимающие значения из множества l₁, l₂,…, l_d. Пусть поступают данные от n меток, поступающие в определенный момент времени одновременно, описываются ситуационным вектором с координатами{x₁, x₂,…, x_n}, представленными лингвистическими переменными: x₁ – энергетика сигнала от метки №1; x₂ - энергетика сигнала от метки №2; и так далее; x_n - энергетика сигнала от метки № n.

Пусть для этого класса наблюдались два прецедента d₁, d₂, каждый из которых применялся в двух (разных) случаях. Лингвистические переменные принимают следующие унифицированные значения (термы): x_i = {статический низкий уровень, статический высокий уровень }, i = 1, …, n.

Допустим, например, матрица знаний для этой системы представлена в табл.2 при n=3.

Таблица 2.

№	Координаты ситуационного вектора			Прецеденты
	x1	x2	x3
1.1 1.2 1.3 1.4	выс. выс. низк. сред.	выс. низк. выс. выс.	выс. сред низк. сред.	d1
2.1 2.2	низк выс.	сред. Низ.	низк. низк.	d2

Пусть наблюдается ПрС/С, описываемая координатами .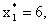

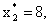
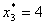Тогда, согласно алгоритму выбора предпочтительного прецедента получим решение в табл.3.

Таблица 3.

№ п/п	Координаты ситуационного вектора			min	max
	x1	x2	x3
1.1 1.2 1.3 1.4	0.6 0.6 0.6 0.9	0.8 0.2 0.8 0.8	0.4 0.8 0.6 0.8	0.4 0.2 0.6 0.8	0.8
2.1 2.1	0.4 0.6	0.4 0.2	0.6 0.6	0.4 0.2	0.4

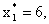
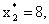
Вывод: наиболее предпочтительным прецедентом ( 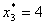) является прецедент d_1.

Литература:

1. Прохоров М. Д. Федунов Б.Е. Вывод по прецеденту в базах знаний бортовых интеллектуальных систем, размещаемых на борту антропоцентрических объектов.

2. Дшхунян В.Л. Электронная идентификация. Бесконтактные электронные идентификаторы и смарт-карты / В.Л. Дшхунян, В.Ф. Шаньгин. – М.: ООО «Издательство АСТ»: Издательство «НТ Пресс», 2004. – 695 с.