Математика/1. Дифференциальные и интегральные уравнения

 

К.ф.-м.н. Тингаев А.А.

Одесский институт финансов УГУФМТ, Украина

Свойства решений сингулярного уравнения 2-го порядка при равных корнях характеристического уравнения

 

Solutions properties of second order singular equation with equal roots of characteristic equation. This article contains the investigation of conditions on which singular second order differential equations have solutions that satisfy to the set estimation. The sufficient conditions of existence of such solutions are obtained.

Свойства решений сингулярного уравнения 2-го порядка при равных корнях характеристического уравнения. Изучается проблема существования решений сингулярных дифференциальных уравне­ний 2-го порядка, удовлетворяю­щих заданной оценке. Получены достаточные условия  существования таких решений.

Постановка задачи. Изучение асимптотических свойств решений дифференциальных уравнений и систем принадлежит к наиболее актуальным задачам качественной теории дифференциальных уравнений, к которым, как известно, сводятся математические модели механики, электротехники, атомной и ядерной физики, физхимии, математической биологии и др. Направления исследований таких уравнений и их систем достаточно разнообразны. Во многих случаях новая задача требует собственных, не традиционных подходов и доказательств фундаментальных теорем.

Анализ последних достижений. Теория диффе­рен­ци­альных уравнений второго порядка в достаточно полном виде появилась в прошлом веке (библиографию можно посмотреть в [1]). Актуальность практических применений повлияла на появление многих видов дифференциальных уравнений второго порядка, которые исследуются по нынешнее время.

Цель статьи. Провести изучение вопроса о существовании решений сингулярных дифференциальных уравнений 2-го порядка, удовлетворяющих заданной оценке вблизи точки сингулярности. Получить достаточные условия существования таких решений.

Изложение основного материала. Рассмотрим уравнение вида

                        (1)

где на (0;∆]; 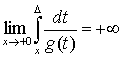 при ∆ > 0; 

  при  x→+0.

Решения уравнения (1) ищутся в полном нормированном про­странстве Хy функций  в котором

a)  , где ,                                                               (2а)

b) .                                                                       (2b)

Так как  при x→+0, то линейное однородное уравнение, соответствующее уравнению (1), имеет асимптотически равные корни характеристического уравнения при x→+0. Поэтому будем искать асимптотики двух видов, соответствующих равным корням характеристического уравнения.

1. Положим 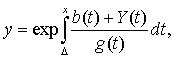 где Y(t) – новая неизвестная функция вместо y(x). Тогда, заметив, что

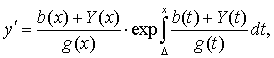
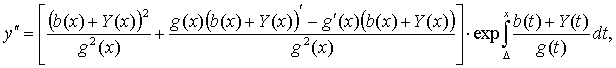
получим для Y(t) сингулярное интегро-дифференциальное уравнение

                  (3)

где .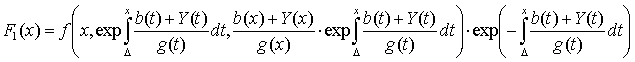

Введём класс функций :

.

Дальнейшие рассуждения основаны на принципе неподвижной точки Шаудера ([2]) и топологическом принципе Важевского ([3]).

Основные предположения и построения

Тоерема 1. Пусть

1)      дифференциальное уравнение

                  ()

удовлетворяет условиям теоремы существования и единственности непрерывного решения в области

D1 =

2)     , причём   что на [0;∆]:

3)      такое, что в D1

а) равномерно ограничены функции ,  и

б) при x→+0:   

Тогда уравнение (3) имеет интегральное многообразие размерности единица из при соответствующем α.

Если вернуться к уравнению (1), то это утверждение означает, что оно имеет интегральное многообразие размерности единица такое, что на (0;∆]:

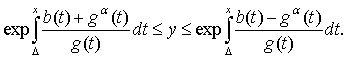
Доказательство.

Воспользуемся принципом неподвижной точки Шаудера. Рассмотрим банахово пространство непрерывных на [0;∆] функций Y(x) с нормой

а в нём – выпуклое, замкнутое, ограниченное множество функций .

Зададим на множестве  оператор А таким образом, чтобы его неподвижная точка была решением уравнения (3).  А именно, произвольной функции  оператор А ставит в соответствие единственное непрерывное на [0;∆] решение Y(x) уравнения (), график которого проходит через произвольную фиксированную точку , где .

Докажем, что оператор А имеет неподвижную точку, то есть такая, что . Для этого, как известно, следует доказать, что а) А отображает множество  в себя; б) множество относительно компактно на ; в) А – непрерывный оператор.

п.1. Для доказательства сначала определим множество

и покажем, что  является множеством строгого входа уравнения () при x→+0.

         Обозначим вектор внешней нормали к  в произвольной ее точке через : , а вектор поля уравнения () в той же точке при  через .          Найдем знак скалярного произведения :

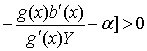
в силу условия 3б). Таким образом, – поверхность строгого входа () при x→+0. Значит,  такая, что ее график проходит через произвольную фиксированную точку . Следовательно, оператор А отображает множество  в себя.

         п.2. Относительная компактность вытекает из теоремы Арцела-Асколи. В самом деле, все функции  равномерно ограничены, поскольку , а . Кроме того, из условия 3а) следует равномерная ограниченность производных функций . Значит, само множество  равностепенно непрерывно.

         п.3. Докажем непрерывность оператора А.

         Пусть  – решение уравнения () при :

                  (4)

Заметим, что если  на [0;∆], то тем более  на [0;∆]. Зададим произвольно малое  и докажем, что  такое, что если

,,

то .

         Вычитая из тождества (4) уравнение (), получим уравнение

                  (5)

         Если теперь доказать, что  такое, что при

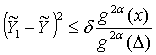
график решения уравнения (5), для которого  оказывается лежащим в , то это будет означать непрерывность оператора А. Для доказательства достаточно показать, что поверхность  является поверхностью строгого входа уравнения (5) при x→+0. Обозначим  – вектор нормали к этой поверхности в произвольной ее точке, а  – вектор поля уравнения (5) в той же точке и определим знак скалярного произведения :

,

если  в силу того, что, согласно условию 3б), при x→+0 .

Таким образом, так как выполнены все условия принципа Шаудера, то существует решение уравнения (3) такое, что

Меняя значение Y0 на интервале , получим многообразие размерности единица решений уравнения (3) из класса .

2. Положим теперь 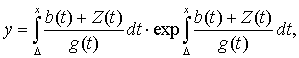 где Z(t) – новая неизвестная функция вместо y(x). Тогда, рассуждая аналогично предыдущему, получим, что выполняется

Тоерема 2. Пусть

1)       =  уравнение

  ()

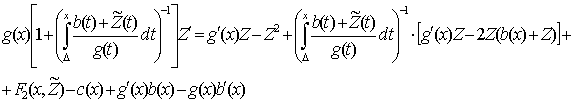удовлетворяет условиям теоремы существования и единственности непрерывного решения в D =

2)     , причём   что на [0;∆]:

3)     такое, что в D

а) равномерно ограничены , ,  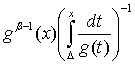и

б) при x→+0:     

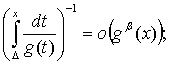
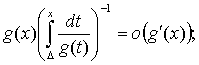
Тогда уравнение

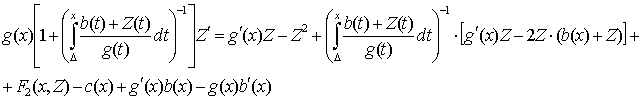
имеет интегральное многообразие размерности единица из  при соответствующем β.

 

Литература

1.     Рейссиг Р, Сансоне Г., Конти Р. Качественная теория нелинейных дифференциальных уравнений. М., Наука, 1974.-320 с.

2.     Хартман Ф. Обыкновенные дифференциальные уравнения: Пер. с англ. - М.: Мир, 1970. - 720 с.

3.     Wazewski T. Sur une principe topologique de l'examen asymptotique des integrales des equations differentielles//Ann. Soc. Polon. Math. - 1947. - Vol. 20, №8.- Р. 279-313.