Mathematics / 3. The theory of probabilities and mathematical statistics

The candidate of the physicist - mathematical sciences Kalzhanov M. U.

Kostanay State University name A.Baitursynov

Measurement forms of distribution laws in the formation of tracks

The peculiarity of the laws of distribution of random variables as the measurement error of the instrument consists of their great variety. This is due to the fact that the overall accuracy of the measuring instrument is determined of a number of components.

In case if the components would be regarded as random values then the summation of errors is reduced to the summation of the random variables. In relation to adding up of casual sizes the laws of their distribution change a form.

The law of sum distribution of independent random variables with distributions p₁x и p₂x, called composition, expressed the convolution integral:

The form's measurement of the laws of distribution at formation of compositions occurs as follows:

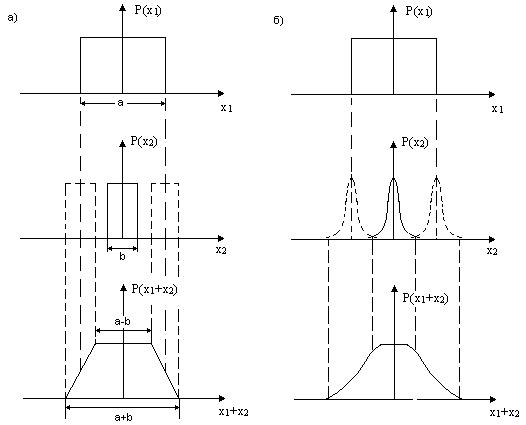
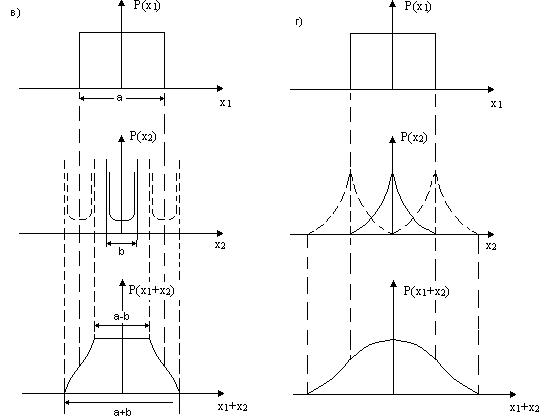
Fig. a) for the summation of the two errors are uniformly distributed with a wide distribution, а > в the resulting error distribution is in the form of a trapezoid with the upper base a-в and a lower-to а+в.

This deformation can be represented as a blurring of sharply limited the wider tails of the distribution (width а) by an amount less than the length of a wide distribution.

The composition of two identical (the width of а) uniform distribution is triangular.

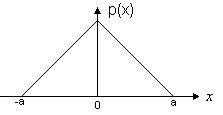
in -a ≤ x ≤ 0

= in 0 ≤ x ≤ а

in -a > x; x >a

This so-called distribution of Simpson. This law of distribution is characteristic for random errors of digital measuring instruments, in which the measured value is converted into a proportional amount of time T_сч, called the computation time. The measurement of this interval is performed by counting pulses stable oscillator having a predetermined repetition period Т_с. The position relative to the interval counting pulses T_сч is random , the ratio between T_сч and T_с is also random, thus the maximum error of these values are equal, i.e. а₁=а₂ => triangular distribution law .

Fig. б) Similarly, the composition is formed by uniform and normal distributions , only the rise and fall of the edges of the resulting distribution curve passes through the integral law of normal distribution.

Fig. в) with a uniform composition distribution and a width with the width arksinusoidalnogo is curved trapezoid with the upper base а-в and a lower - to а+в and troughs for curves integral law arcsin- distribution.

Fig. г) Song uniform and Laplace distribution (two-sided exponential) has a long, hollow decaying "tails" of the curve of the resulting distribution.

The sheer scale of the curves in figure а-г is determined each time the fact that the area under the curve of any of the density distribution should be equal to 1.

References:

1. A.D. Wentzel A course of lectures on casual processes . М., Science, 1982.

2. E.S. Wentzel, A.V. Ovcharov. Applied problems in the theory of stochastic processes. М., Science, 1992.