Математика / 3. Теория вероятностей и математическая
статистика
к.ф.-м. н. Калжанов М.У.
Костанайский государственный университет
имени А.Байтурсынова
Свойства
многомерного нормального распределения
Все одномерные плотности
вероятности - это плотности вероятности одномерной нормальной случайной
величины с параметрами, определяемыми координатами вектора X и главной
диагональю ковариационной матрицы B. Кроме того, подвектор вектора ![]() из k элементов, где
из k элементов, где ![]() также распределен нормально.
также распределен нормально.
Если все коэффициенты
корреляционной или ковариационной матрицы B (все ее недиагональные элементы)
равны нулю, то показать самим, что компоненты случайной величины являются
независимыми.
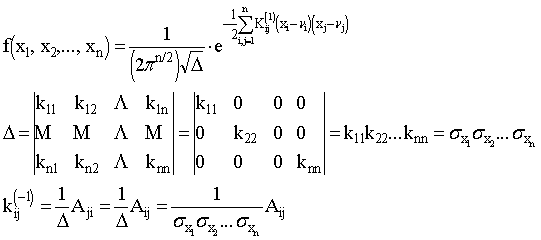
если ![]() ,то многомерная плотность распадается на произведение одномерных,
значит
,то многомерная плотность распадается на произведение одномерных,
значит ![]() независимы.
независимы.
Теорема.
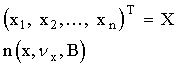
Проводим линейное
преобразование Y=AX. A - квадратная невырожденная матрица, тогда вектор Y также
имеет n-мерное нормальное распределение вида
![]()
Следствие: Из теоремы вытекает, что ковариационная матрица
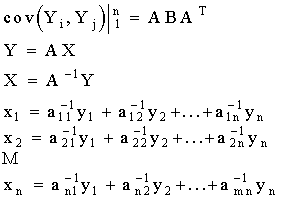
Оператор A переводит
произвольную область из арифметического пространства Rn в некоторую
область того же пространства.
Рассмотрим произвольную
область S, принадлежащую пространству элементарных событий случайной
многомерной величины X. Ей соответствует область D в пространстве элементарных
событий случайного вектора Y. При этом
![]()
Запишем эти вероятности
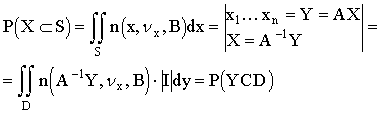
где |I| - якобиан перехода
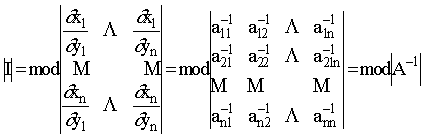
Т.к. область S и
соответственно D произвольны, то плотность вероятности случайного вектора x
равна
![]()
n-мерная плотность вероятности
случайного вектора Y равна
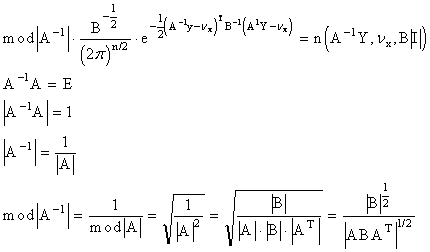
Преобразуем показатель степени
e
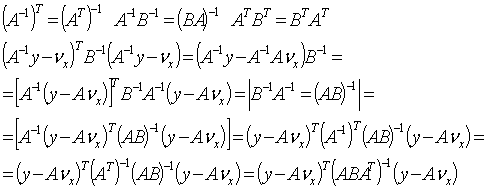
Можно показать, что если
нормальное распределение имеет данный вид, то B - ее ковариационная матрица
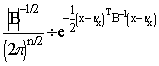
Следствие.
![]() - многомерный нормальный вектор. A - прямоугольная матрица
- многомерный нормальный вектор. A - прямоугольная матрица ![]() Тогда Y=AX имеет
нормальное распределение вида
Тогда Y=AX имеет
нормальное распределение вида
![]()
Y - m-мерный вектор.
Для определенности положим,
что матрица A имеет вид
A = (A1 A2)
A1 - квадратная
матрица размером ![]()
A2 - матрица
размерности ![]()
Считается, что m первых
столбцов независимы.
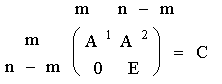
![]() равен определителю
полученной квадратной матрицы и не равен нулю.
равен определителю
полученной квадратной матрицы и не равен нулю.
E - единственная квадратная
матрица размерности ![]()
Следовательно, на основании
доказанной теоремы, вектор Y имеет многомерное нормальное распределение.
Z=CX
Компоненты вектора Z имеют вид
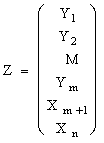
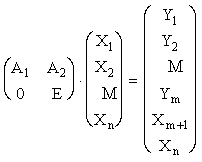
Литература :
1. Вентцель Е.С., Овчаров А.В.
Прикладные задачи теории случайных процессов. М., Наука, 1992.
2. Гихман И.И., Скороход А.В.
Введение в теорию случайных процессов. М., Наука, 1972.