Математика/ 3. Теория вероятностей и математическая статистика

Агаева Ф.И., к.ф.-м.н. Искакова А.С.

Евразийский национальный университет им. Л.Н. Гумилева, Казахстан

Вероятности стратегий в моделях тестовых заданий

Выполнение тестов человеком, не знакомым с предлагаемым набором вопросов, можно предсказать с погрешностью, поддающейся вычислению, даже если давать испытуемым разные тесты, с вероятностью угадывания ответа: . где n – число вариантов.

 Результаты эмпирических исследований показали, что, чем ниже уровень способностей испытуемого (низкие значения параметра в), тем чаще он прибегает к стратегии угадывания. Аналогично, чем труднее задание, тем больше вероятность того, что испытуемый будет пытаться угадать правильный ответ, а не решать задачу.

Бирнбаум предложил трехпараметрическую модель, которая позволила бы учесть влияние угадывания на результат выполнения теста.

Трехпараметрическая модель Бирнбаума выглядит так:

.

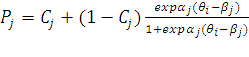 Соответственно оценка “силы” пункта (трудности задания) в логистической форме модели

,

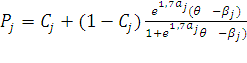где C_j характеризует вероятность правильного ответа на задание j в том случае, если испытуемый угадывал ответ, а не решал задание. Для заданий с пятью вариантами ответов С становится более пологой, так как 0 < С < 1, но при всех С = 0 кривая поднимается над осью q на величину С_j . Тем самым даже самый неспособный испытуемый не может показать нулевой результат. Дифференцирующая сила тестового задания при введении параметра С_j снижается. Из этого следует нетривиальный вывод: тесты с “закрытыми” заданиями (вынужденным выбором ответа) хуже дифференцируют испытуемых по уровням свойства, чем тесты с “открытыми” заданиями.

Модель Бирнбаума не объясняет парадоксального, но встречающегося в практике тестирования феномена: испытуемый может реже выбирать правильный ответ, чем неправильный. Таким образом, частота решения некоторых заданий может не соответствовать предсказаниями модели Р_j < С_j, тогда как, согласно модели Бирнбаума, в пределе Р_j= С_j.

Рассмотрим еще одну модель, которую предложил В. С. Аванесов. Как мы уже заметили, в IRT не решается проблема валидности: успешность решения задачи зависит в моделях IRT только от одного свойства. Иначе говоря, каждое задание теста считается априорно валидным.

Аванесов обратил внимание на это обстоятельство и ввел дополнительный, четвертый, параметр, который можно обозначить как внутреннюю валидность задания. Успешность решения задания определяется не только “основной” способностью (q), но и множеством условий, нерелевантных заданию, однако влияющих на деятельность испытуемого.

Четырех параметрическая модель представляет, по мнению ряда исследователей, лишь теоретический интерес:

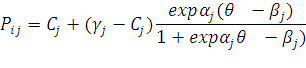
где β_j – валидность тестового задания.

Если β_j > 1, то тест не является абсолютно валидным. Следовательно, вероятность решения задания не только определяется теоретически выделенным свойством, но и зависит от других психических особенностей личности.

Бирнбаум считает, что количество информации, обеспеченное j-м заданием теста, при оценивании q_j является величиной, обратно пропорциональной стандартной ошибке измерения данного значения q_j j-м заданием. Более подробно вычисление информационной функции рассмотрено в работе М. Б. Челышковой.

Многие авторы, в частности Пол Клайн, отмечают, что IRT обладает множеством недостатков. Для того чтобы получить надежную и не зависимую от испытуемых шкалу свойств, требуется провести тестирование большой выборки (не менее 1000 испытуемых). Тестирование достижений показывает, что существуют значительные расхождения между предсказаниями модели и эмпирическими данными.

Главный же недостаток IRT – игнорирование проблемы валидности. В психологической практике не наблюдается случаев, когда ответы на задания теста были бы обусловлены лишь одним фактором. Даже при тестировании общего интеллекта модели IRT неприменимы.

Клайн рекомендует использовать модели IRT для коротких тестов с валидными заданиями (факторно простые тесты).

В пособии Клайна (см. [1]) приведен алгоритм конструирования тестов на основе модели Раша.

Рассмотрим вероятностную модель тестов “уровня” Ф. М. Юсупова (см. [2]). Его модель разработана для тестов с “закрытыми” заданиями (выбором ответов из множества), различающимися по уровню трудности. В “закрытых” тестах испытуемый может применить стратегию “угадывания” ответа. Вероятность угадывания P=1/m, где т – число альтернатив.

Сложность тестового задания W=n/N, где n – число испытуемых, способных решить задание, N – общее количество испытуемых в выборке валидизации.

При W < Р невозможно определить, решена задача случайно или закономерно. Предполагается, что биноминальное распределение вероятности успешного выполнения тестового задания при больших N аппроксимируется нормальным.

Тем самым тестовое задание стимулирует испытуемого к выбору правильного ответа.

Предельно возможное число заданий в тесте выбирается при условии, что различие в уровне их сложности гарантируется с выбранной вероятностью.

Поскольку дисперсия биноминального распределения максимальная в центре интервала 0 – 1 и уменьшается к периферии до 0, шаг градаций сложности на разных участках этого интервала будет различным: на периферии он должен стремиться к нулю.

Удобно принять в качестве шага градации сложности 1/10 интервала. Для a= 0,05, N = 100 получается 7 значений показателя сложности, что при шаге, равном 0,1, гарантирует различение между уровнями с вероятностью 0,9.

Если учесть условие минимизации случайного выбора правильного ответа, то число градаций сложности должно быть еще меньше. Например, при 6 вариантах ответа число заданий разного уровня сложности не может быть больше 6.

Эти выводы верны в том случае, если биноминальное распределение аппроксимируется нормальным распределением. При большом числе испытуемых такая аппроксимация возможна.

Расчеты показывают, что минимально необходимый объем выборки для апробации тестовых заданий не так уж и велик – 56 человек при достоверности 0,9.

Следовательно, исходя из вероятностной модели теста и не прибегая к допущениям о моделях тестирования, можно рассчитать параметры теста как предельные характеристики, обеспечивающие достоверность измерения.

1. П. Клайн. Справочное руководство по конструированию тестов: Введение в психометрическое проектирование: Перевод с английского / Под ред. Л.Ф. Бурлачука. Киев: ПАН Лтд., 1994. 288 с.

2. Дружинин В.Н. Структура и логика психологического исследования. М.: Ин-т психологии, 1993.