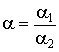КЛАССИФИКАЦИЯ ОБЪЕКТОВ УПРАВЛЕНИЯ
ПО ИХ ТЕХНИЧЕСКИМ ХАРАКТЕРИСТИКАМ
Таишева А.Р., Гарькина И.А.
Пензенский государственный университет
архитектуры и строительства
![]() ,
, 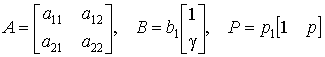
Обычно функционал качества ![]() для системы
для системы ![]() принимается в виде:
принимается в виде:
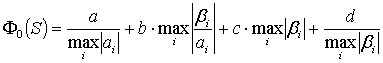 ,
,
где ![]() -
соответственно векторы фазовых координат управляющих и возмущающих воздействий,
-
соответственно векторы фазовых координат управляющих и возмущающих воздействий,
![]() - собственные
числа матрицы А,
- собственные
числа матрицы А,
![]() - весовые константы. Разбиение объектов на
классы (области
- весовые константы. Разбиение объектов на
классы (области ![]() ) осуществляется по
линиям уровня
) осуществляется по
линиям уровня ![]() :
: ![]() .
.
Для системы ![]() (
(![]() ) аналогичный функционал будет иметь вид:
) аналогичный функционал будет иметь вид:
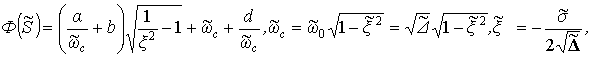
где ![]() - собственная
частота и коэффициент демпфирования замкнутой
системы
- собственная
частота и коэффициент демпфирования замкнутой
системы ![]() .
.
Опишем одним функционалом как колебательные, так и апериодические
системы. Для этого вместо функционала ![]() , описывающего колебательные системы
, описывающего колебательные системы ![]() , введем функционал
, введем функционал
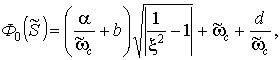
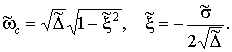
Здесь ![]() уже может принимать
любые действительные неотрицательные значения и может использоваться и для
апериодических систем с
уже может принимать
любые действительные неотрицательные значения и может использоваться и для
апериодических систем с ![]() :
:
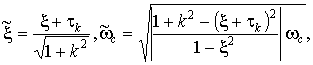
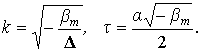
Можно показать (рис.1,2), что при малых k
с увеличением коэффициента k происходит сдвиг
системы на плоскости ![]() :
:
- вправо-вверх, если 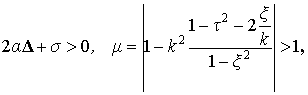
- влево-вверх, если ![]()
- вправо-вниз, если ![]()
- влево-вниз, если ![]() .
.
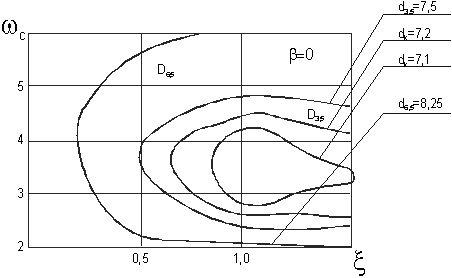
Рис.
1. Зависимости ![]() при разных значениях d
при разных значениях d
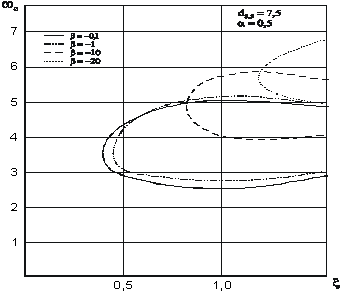
Рис.
2. Зависимость ![]() при различных значениях b
при различных значениях b
Полученные зависимости использовались при разработке имитаторов транспортных систем [1].
Литература
1.
Гарькина И.А.,
Данилов А.М., Пылайкин С.А. Тренажеры и имитаторы транспортных систем: выбор
параметров вычислений, оценка качества / Мир транспорта и технологических
машин.–№3(42).–2013.–С.115-121.
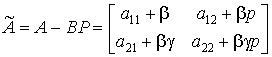 .
.