Математика/ 5. Математическое моделирование
Агаева Ф.И., к.ф.-м.н. Искакова
А.С.
Евразийский
национальный университет им. Л.Н. Гумилева, Казахстан
Механизм оценивания
однопараметрической модели Раша
Разработка
модели Раша связана с попыткой создания стандартизированных шкал, нормативные
показатели которых были бы независимы от конкретной выборки стандартизации.
Выполнение
тестов человеком, не знакомым с предлагаемым набором вопросов, можно
предсказать с погрешностью, поддающейся вычислению, даже если давать испытуемым
разные тесты.
В модели
Раша представляется расчет вероятности того, что случайно выбранный из группы
человек ответит на вопрос правильно, которая
равнялась доле тех, кто дал верный ответ, в общем числе ответивших на
данный вопрос. Этот показатель называется у Раша уровнем трудности задания.
Затем введется расчет логарифма отношения вероятностей правильного и
неправильного ответов. Если трудность задания была 65%, то это означает, что
35% респондентов ответили правильно, а 65% — неправильно. Отношение вероятности
ответить правильно к вероятности ответить неправильно 0,55, а натуральный
логарифм 0,55 составляет -0,62.
Затем Раш
проделал ту же процедуру с вероятностью, что этот человек ответит правильно на
любой вопрос. Поскольку данный респондент давал правильные ответы в 82%
случаев, соответствующий логарифм составил ln(0,82/0,18), или 1,52. Наконец,
Раш сложил значения двух логарифмов и получил: (-0,62) + 1,52 = 0,9.
В результате
получится 71%. Это означает, что есть 71%-ная вероятность того, что данное лицо
ответит на этот вопрос верно, учитывая трудность задания и правильность его
ответов на другие вопросы. При большом числе вопросов и (или) большом числе
испытуемых мы обнаружим следующее: когда уровень трудности задания 70% (то
есть, вероятность получить правильный ответ 30%), около 30% людей ответят на
этот вопрос верно; когда уровень трудности задания 80%, около 20% людей ответят
на данный вопрос верно, и т.д.
Классическая
теория тестирования, несмотря на хорошо разработанный математический аппарат,
прозрачность и ясность получаемых выводов, имеет принципиальные
недостатки. В частности, тестовые баллы испытуемых зависят от трудности заданий
в тесте, а трудность задания зависит от выборки испытуемых. Большим недостатком
классической теории является нелинейность тестовых баллов испытуемых. За
рубежом уже несколько десятилетий развивается современная теория тестирования –
Item Response Theory (IRT), являющаяся частью более общей теории
латентно-структурного анализа. Отдельно следует указать теорию Георга Раша (G.
Rasch), которую иногда называют однопараметрической (теорией) IRT.
В качестве
математической модели, связывающей успех испытуемого с уровнем его
подготовленности и трудностью задания в модели Раша выбирается функция:
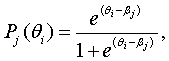 (1)
(1)
где θi – уровень подготовленности, βj – трудность задания
Поскольку
модель Раша описывает вероятность успеха испытуемого как функцию одного
параметра (θi – βj), то в некоторых источниках ее называют
однопараметрической моделью IRT. Взаимодействие двух множеств θi и
βj образует данные, обладающие свойством «совместной
аддитивности» (conjoint additivity). Правильное использование модели Раша
позволяет отделить оценки испытуемых от оценок трудности заданий и наоборот.
Это свойство Rasch Measurement носит название separability
parameter estimates – «независимость оценок заданий от испытуемых и
оценок испытуемых от параметров заданий».
Очевидно, что уровень трудности задания βj на практике является некоторым
сложной определенной величиной. Следовательно формула
(1) не находит фактического применения. В связи с этим возникает необходимость определения оценки вероятности
(1).
Пусть Х=(X1, ..., Xk) представляет выборку
объема k и х=(x1, ..., xk) есть наблюдавшиеся
значения Х, где элементы хi (i=1,
…, k) указывают правильность
ответа i-го тестируемого
студента, то есть хi принимает значение 0 или 1. Разобьем выборку на
две выборки с объемами k1 и k2, где k1 – количество студентов,
ответивших правильно и k2 – ответивших неправильно. Допустим, что выборка
формируется из группы студентов подготовленности θ1 и θ2,
причем θ1 > θ2 и θ1+θ2=1.
Рассмотрим
оценку максимального правдоподобия для параметра βj,
которая как известно обладает хорошими асимптотическими свойствами.
На основании предпоожений имеем следующую функцию
правдоподобия распределения (1)
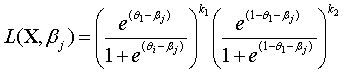
и соответственно
логарифмическую функцию правдоподобия имеет вид
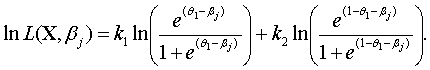
Следовательно,
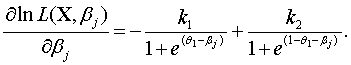
В силу метода
максимального правдоподобия
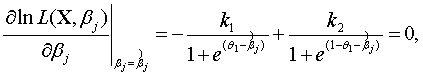
где ![]() - оценка максимального правдоподобия параметра βj. Решая последнее уравнение
имеем
- оценка максимального правдоподобия параметра βj. Решая последнее уравнение
имеем
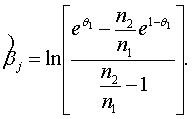
Таким
образом,
задача построения оценки трудности задания решена.
Литература:
1. Леонова Н.М. Параметрически адаптивное управление
образовательной деятельностью: монография под ред. А.Д. Модяева. (Серия
“Социальная кибернетика”). М.: МИФИ, 2006.
2. Челышкова М.Б. Теория и практика конструирования
педагогических тестов: учебное пособие. М.:
Логос, 2002.
3. Masters N.
G. The Key to Objective Measurement.
Australian Council on Educational Research, 2001.
4. Masters N.G.
A Rasch Model for Partial Credit Scoring.
University of Chicago, Psycometrika, 1982. V. 47. № 2.
5. Lord F.M. // Journal of Educational Measurement. 1977. V. 14. P. 117.
6. Hambleton K. R., Jones
W. R. An NCME instructional module on Comparison of Classical
Test Theory and Item Response Theory and Their Application to Test Development.
University of Massachusetts at Amherst, 2003.
7. Tang K. Linda. Polytomous Item Response Theory Models and Their Application in
Large-Scale Testing Programms // Review of Literature. Educational Testing
Service, Princeton, New Jersey, 1996.
1