Математика / 5. Математическое моделирование

К.т.н. Колдаев В.Д.

Национальный исследовательский университет МИЭТ, Россия

Организация данных в адаптивных системах распознавания изображений

Процесс предварительной обработки изображений зависит от выбора целевых признаков, которые могут быть представлены совокупностью границ (контуров), определяющих их внутреннюю структуру, отделяющих их от фона и других объектов. Контуры изображения представляются максимальными перепадами значений интенсивности, которые являются характерными признаками объектов. Структура организации обработки и анализа изображений в автоматизированных производственных системах (АПС) представлена на рис.1.

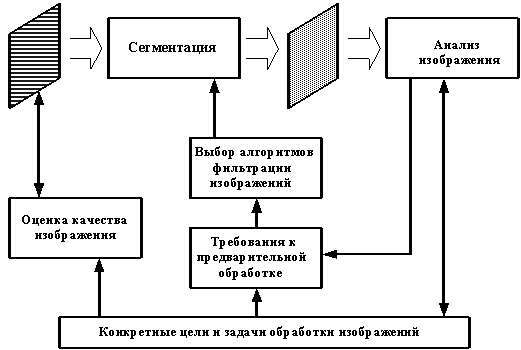
Рис.1. Организация обработки и анализа изображений в АПС

Для организации данных в адаптивных системах распознания изображений следует использовать структурное представление, при котором форму объекта можно представить в виде набора примитивов (неделимых в рамках данного применения элементов), иерархического набора базисных элементов (полученных комбинаций примитивов и базисных элементов низких уровней) и спецификации отношений этих элементов [1].

В АПС особая роль отводится методам выделения свойств объекта с целью распознавания. Существующие системы основываются на трех основных категориях дескрипторов: площадь области, определяемая как число пикселей, содержащихся в пределах границы; отношение длин большой и малой осей, называемое эксцентриситетом области; периметр области. В идеальном случае дескрипторы не должны зависеть от размеров, расположения и ориентации объекта, но должны содержать достаточное количество информации для надежной идентификации объектов.

Методы аппроксимации контуров ломаной линией. В методе полигональной аппроксимации итеративно строится такой многоугольник, который содержал бы минимальное число вершин и в то же время представлял фигуру с заданной точностью (рис.2,а).

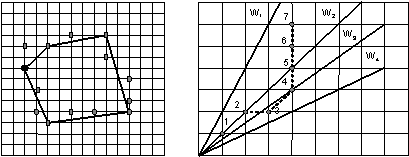
а б

Рис.2. Полигональная аппроксимация (а) и построение ломаной контура (б)

Метод аппроксимации контуров заданными кривыми предполагает представление анализируемых фигур в виде набора стандартных фигур, близких к аппроксимируемым по форме и размерам (прямоугольник, эллипс, ромб, равнобедренный треугольник). Тогда для дискретного замкнутого контура B = {b₁, b₂,…,b_n} с координатами контурных точек b_i = (x_i, y_i) из множества стандартных фигур подбирается такая, для которой сумма квадратов расстояний до точек контура минимальна.

При построении отрезка ломаной контура из начала координат проводятся лучи через соседние с (x_i, y_i) точки реестра (рис.2,б). Лучи W_j выбираются таким образом, чтобы образованный ими угол имел максимальное значение. Номер луча равен номеру вершины, вносящей соответствующее ограничение на область, которой должен принадлежать узел аппроксимации.

Методы параметрического задания контуров. При полярном кодировании контуров осуществляется сканирование контуров из центра масс радиальными лучами через равные углы. Длина радиус-вектора между центром масс и точкой пересечения с контуром используется как элемент одномерного массива R(θ_i) (рис.3,а). Одномерное описание контура получается при использовании метода кодирования направлений. Компактное представление плоских кривых получается при использовании цепного кодирования, предложенного Х. Фрименом (рис.3,б).

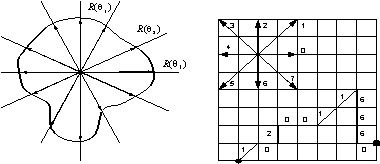
а б

Рис.3. Полярное кодирование контура (а) и цепной код (б)

Подвижная координатная система, созданная на базе цепного кода, обеспечивает инвариантность описаний относительно операций параллельного переноса.

Разработанные в НИУ МИЭТ [2] угловые коды, обладая инвариантными свойствами относительно операций переноса и поворота, обеспечивают получение обобщенных характеристик для представления контуров изображений (рис.4).

Пусть – угловой код длины m; S_i – i-й элемент кода (для прямоугольной решетки {2,3,4,5,6}). Прямая, совпадающая с вертикалью, горизонталью или диагональю, задается в угловом коде последовательностью элементов прямоугольной решетки.

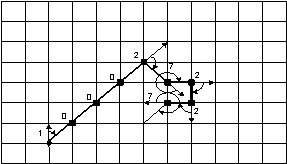
Рис.4. Метод углового кодирования контура

Отклонение от прямой для i-й точки кода равно: Оценить кривизну i-го элемента можно как

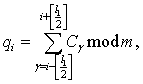
где l₁ – длина кодовой записи, на которой рассчитывается кривизна. При вычислении кривизны для всех точек контура участком длиной l₁ осуществляется сканирование вдоль всего углового кода контура. Отсюда получаем:

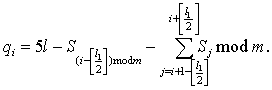
Для следующего элемента кода:

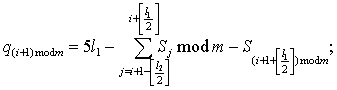
Сравнивая выражения, получаем оценку кривизны в рекуррентном виде:

Оценка q представляет собой сумму отклонений C на участке контура l₁ (все отклонения суммируются с единичными весами). Изменять веса можно, используя оценку кривизны второго порядка, для получения которой участок длиной l₂ сканирует вдоль полученной ранее оценки q:

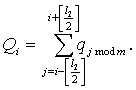
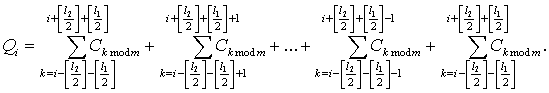
Величина Q_i представляет собой сумму отклонений с весами, возрастающими от единицы до центра участка сканирования. Максимальный вес в центре участка сканирования достигает величины . Длина участка сканирования при этом равна , а количество отклонений в центре участка сканирования составляет .

Рассматривая оценку кривизны более высоких порядков, учитываются отклонения точек с различными весами:

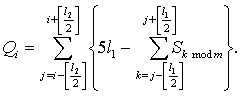
В итоге получаем рекуррентную формулу, связывающую Q_i и Q_i+1:

Метод топологического задания контуров. Метод основан на разбиении контура на секции, в которых линия монотонно возрастает или убывает по x и по y. Горизонтальная или вертикальная линия пересекает такую секцию только в одной точке. На рис.5,а представлены два различных случая пересечения секций, в одном случае секции пересекаются только в одной точке, в другом – в нескольких точках. На рис.5,б серым цветом выделены условия, при которых можно применять метод поиска пересечений контуров.

а	б

Рис.5. Алгоритм определения пересечения полилиний: а) различные варианты пересечения секций; б) схема определения единственности

точки пересечения секций

Наличие разнообразных способов описаний изображений приводит к определению общих свойств, которыми они должны обладать: компактность; сохранение топологических и геометрических свойств объекта; возможность определения различных характеристик объекта на языке описания; возможность обратного восстановления; инвариантность относительно операций переноса и поворота; возможность получения описания параллельным способом.

Литература

1. Колдаев В.Д. Анализ контурной сегментации изображений в автоматизированных производственных системах [Текст] / В.Д. Колдаев // Оборонный комплекс – научно-техническому прогрессу России: Межотраслевой научно-технический журнал. – М.: ФГУП «ВИМИ», 2008. – Вып.4. – С.54-59.

2. Колдаев В.Д. Растровые модели систем обработки изображений [Текст] / В.Д. Колдаев // Сборник материалов 1-й международной научно-практической конференции «Интеграция науки и производства». – Тамбов, 2008. – С.111-113.