Математика/ 5. Математическое моделирование
Д.т.н. Шацкий
В.П., к.т.н. Федулова Л.И., к.ф.м.н. Гриднева И.В.
Воронежский
государственный агроуниверситет им. Петра I, Россия.
К вопросу об учете третьей координаты при моделировании работы водоиспарительных
охладителей
На сегодняшний день перспективность
водоиспарительных охладителей, как экономичных и экологически чистых,
безусловна. Повышение эффективности работы таких установок не возможно без
математического моделирования внутренних процессов, протекающих в каналах
теплообменных насадок. Однако построенная и реализованная двумерная
математическая модель предполагает постоянство температуры и плотности пара по
высоте канала. Но в ряде случаев, материал, используемый в пластинах, обладает
маленьким фитильным эффектом, и в
случае нижнего орошения ширина и высота каналов становятся соизмеримы, следовательно
влияние третьей (вертикальной) составляющей существенно. Таким образом,
необходимо пространственное моделирование теплообменных процессов в каналах
испарительных насадок.
Рассмотрим пространственную математическую
модель прямого охлаждения, построенную на базе имеющейся плоской модели с
подключением соответствующих начальных и краевых условий. Физические условия в
каналах одинаковы, b – сечение канала.
Уравнения энергии и уравнение переноса
массы в канале
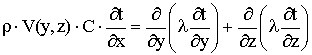 (1)
(1)
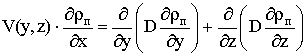 (2)
(2)
Здесь t – температура воздуха, ![]() - плотность пара,
φ – относительная влажность воздуха,
- плотность пара,
φ – относительная влажность воздуха, ![]() - плотность пара на
линии насыщения, определяемая по формуле
- плотность пара на
линии насыщения, определяемая по формуле ![]() . V(y,z) –
скорость потока воздуха, λ и D – соответственно коэффициенты теплопроводности воздуха и
диффузии пара, x, y и z– соответственно координаты по длине,
ширине и высоте каналов.
. V(y,z) –
скорость потока воздуха, λ и D – соответственно коэффициенты теплопроводности воздуха и
диффузии пара, x, y и z– соответственно координаты по длине,
ширине и высоте каналов.
Начальные условия – параметры воздуха на входе в каналы (Это температура
поступающего в охладитель воздуха ![]() и плотность
содержащегося в нем пара, определяемая по относительной влажности
и плотность
содержащегося в нем пара, определяемая по относительной влажности ![]() )
)
![]() ,
,
![]() (3)
(3)
Граничные условия на мокрой поверхности
пластин
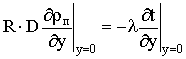 ,
,
![]() , (4)
, (4)
где
R=(2500.6–2.372×t)×103, дж/кг – удельная теплота
парообразования.
На оси симметрии канала
выполняется условие четности:
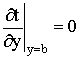 ,
, 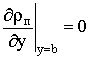 (5)
(5)
Условия непроницаемости на верхней границе.
(Верхней границей каналов является крышка охладителя, которая обладает хорошим
теплоизолирующим свойством и не проницаема для пара)
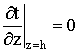 ,
, 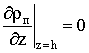 (6)
(6)
Рассматриваются охладители, пластины
которых имеют оребрение, и нижней горизонтальной поверхностью каналов (z=0) является смоченная поверхность оребрения.
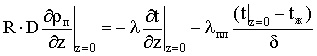 ,
,
![]() . (7)
. (7)
Скорость в каналах описывается
уравнением
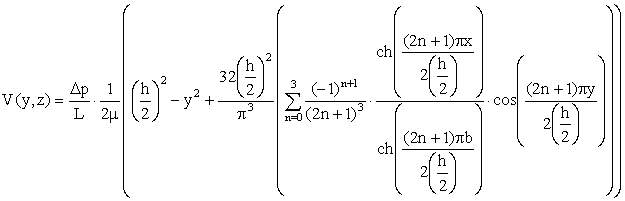 ,
,
где L – длина пластин насадки, ![]() - динамическая вязкость.
- динамическая вязкость.
Указанная математическая
модель представляет собой систему квазилинейных дифференциальных уравнений в
частных производных параболического типа и не имеет аналитического решения. Данная модель была численно реализована с
использованием неявных схем решения уравнений параболического типа с включением
отрицательных источников тепла в граничные условия и применения метода
продольно-поперечной прогонки.
Проведенный сравнительный анализ
результатов расчета по трех и двумерным моделям показал, что представленная
пространственная модель существенно уточняет описание процессов тепломассопереноса
в каналах насадок испарительного теплообменника прямого принципа действия.
Кроме того, в ходе расчета по трехмерной модели было установлено, что
существуют вполне определенные зависимости эффективности работы охладителей от
различных факторов, к которым относятся основные конструкторские характеристики
установок.
Литература:
1. Шацкий В.П.
Моделирование теплофизических процессов в водоиспарительных теплообменниках /
В.П. Шацкий., Л.И Федулова, И.В. Гриднева //Информатика: проблемы, методология,
технологии: материалы XII Международной научно-методической конференции,
ВГУ.-Воронеж, 2013.- С. 436-440.