МЕТОД АППРОКСИМАЦИИ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
Хнаев О.В., Данилов А.М.
Пензенский
государственный университет архитектуры и строительства
Приводится методов аппроксимации функции многих
переменных 
, основанный на использовании метода планирования эксперимента [1]. В результате
анализа представленной информации
удалось выявить переменные 
, принимающие только два значения (нижний и верхний уровни;
используются индексы «н» и «в» соответственно).
Введем
, 
, 
;
, 
, 
;
, 
, 
.
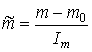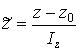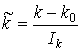Предполагается:
, 
; 
, 
; 
, 
;
, 
; 
, 
;
, 
.
Кодированные
значения нижних и верхних уровней переменных будут равны 
, 
, а для центра эксперимента
- 
.
Будем искать аппроксимационную модель в
виде
.
Воспользуемся ортогональной матрицей
планирования (вид в натуральных переменных – табл.1). Следствием
ротатабельности матрицы является равная точность линейной модели во
всех направлениях относительно центра (
).
В кодированных переменных получим модель вида
,
,
,
.
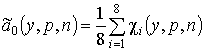Таблица 1. Матрица планирования
|
№ опыта |
|
|
|
|
|
1 |
0,15 |
20 |
0 |
|
|
2 |
0,4 |
20 |
0 |
|
|
3 |
0,15 |
35 |
0 |
|
|
4 |
0,4 |
35 |
0 |
|
|
5 |
0,15 |
20 |
32 |
|
|
6 |
0,4 |
20 |
32 |
|
|
7 |
0,15 |
35 |
32 |
|
|
8 |
0,4 |
35 |
32 |
|
Переходя
к натуральным переменным, получим
;
,
.
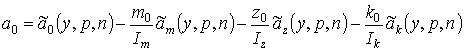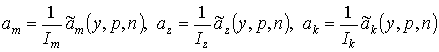При
фиксированных значениях p и n коэффициенты модели будут функциями одной
переменной y (табл. 2).
В дальнейшем после аппроксимации коэффициентов 
полиномами Лагранжа была получена модель
,
,
,
,
.
Таблица 2. Значения коэффициентов при p =40 и n=20.
|
y |
0,5 |
0,7 |
1,0 |
1,1 |
|
|
0,0697 |
0,0620 |
0,0543 |
0,0354 |
|
|
0,0100 |
0,00650 |
0,0110 |
0,0380 |
|
|
-0,00063 |
-0,00036 |
0,00025 |
0,0013 |
|
|
0,00033 |
0,000707 |
0,00128 |
0,00136 |
Если полученные модели в выбранных интервалах
варьирования факторов окажутся не адекватными, то возможны их уточнения с
учетом эффектов взаимодействия:
.
Таким образом, для фиксированных значений p и n по матрицам планирования
будет осуществлена аппроксимация функции 
, как функции четырех переменных.
Приведенная методика эффективно использовалась
для подготовки баз данных имитаторов динамики полета (уточнение на каждом шаге
интегрирования начальных условий задачи Коши при решении уравнений динамики
полета методом Рунге-Кутта).
Литература
1.
Гарькина
И.А., Данилов А.М. Прошин А.П., Соколова Ю.А. Планирование эксперимента.
Обработка опытных данных: монография. Под ред. проф. А.М.Данилова. – М.:
Палеотип. – 2005. – 272 с.
2. Данилов А.М., Гарькина
И.А., Домке Э.Р. Математическое и компьютерное моделирование сложных систем. -
Пенза: ПГУАС, 2011. -296 с.