ТРАНСПОРТНАЯ ЗАДАЧА ПРИ НЕОПРЕДЕЛЕННОМ СПРОСЕ

Маркелова И.В., Гарькина И.А.

Пензенский государственный университет архитектуры и строительства

В последние годы при решении экономических задач широко используются стохастические модели. Это, прежде всего, решаемые методами математического программирования задачи со случайными параметрами (предмет стохастического программирования). В некоторых случаях при решении стохастических задач случайные величины еще до начала решения задачи заменяются усредненными значениями, и оптимизируется не сама функция цели, а ее математическое ожидание. Однако такой прием, означающий, что случайный процесс заменяется его детерминированной моделью, оказывается применимым далеко не всегда. Он дает хорошие результаты только тогда, когда рассматриваемая система состоит из достаточно многочисленных объектов и когда случайные отклонения каждого из них взаимно компенсируются.

Задачи, в которых некоторые параметры могут быть случайными величинами, разбиваются на два класса: одношаговые и многошаговые задачи. Ограничимся рассмотрением одношаговых задач на конкретном примере. Пусть однородный товар размещен на складах и допустимое количество товаров на -м складе есть . Товар следует транспортировать в магазинов. При этом спрос в каждом магазине заранее точно не известен. Однако известно, что потребности этих магазинов следует считать непрерывными случайными величинами с плотностью вероятности , где -номер магазина и - потребность этого магазина.

Предполагается, что значения - независимые случайные величины, то есть магазины расположены таким образом, то спрос в каждом из них не влияет на спрос в других магазинах.

Обозначив через стоимость перевозки единицы товара со склада в магазин . Полную стоимость перевозки будем считать пропорциональной количеству перевозимого товара . Пусть - количество товара, поступившего в -ый магазин. Если это количество меньше спроса , то магазин не получим той выручки, которую мог бы получить (не говоря уже о потерях населения от неудовлетворительного спроса). В предложении линейности потери -го магазина от недостаточного объема доставки товара будут равны , где . Если , то магазин также терпит убыток, в частности, из-за того, что необходимо отправлять товар обратно на склад или продавать его по сниженной цене. Пусть получившийся в этом случае убыток есть , где . В этих условиях требуется определить наивыгоднейшее количество поставляемого каждому магазину товара , при котором сводятся к минимуму транспортные расходы и возможные убытки от избытка или недостатка товаров при наличии случайного спроса. Средние ожидаемые потери из-за нехватки товаров в -м магазине определятся математическим ожиданием случайной величины :

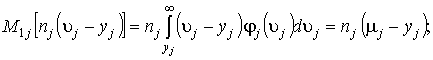
, (1)

где 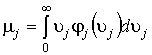- ожидаемый спрос в -м магазине (все ).

Аналогично средние ожидаемые потери, вызванные избытком товаров в-м магазине, будут равны

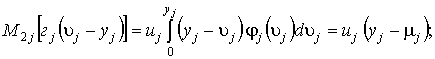
. (2)

Тогда полные затраты, включая транспортные расходы и ожидаемые потери из-за недостатка или избытка товаров во всех магазинов, составят:

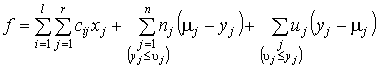(3)

Отметим, что два последних члена в (3) никогда не будут встречаться вместе, поскольку недостача и избыток товара не могут возникнуть одновременно. Окончательно исходную задачу можно сформулировать следующим образом: при ограничениях

(4)

найти

.

(5)

Отметим, что обратный переход от стохастической задачи (4) – (5) к соответствующей линейной транспортной задаче с постоянными параметрами легко осуществляется. Если положить (при условии, что ), то мы сразу придем к задаче: при ограничениях 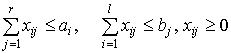найти .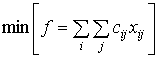

В этой задаче два ограничения, как и в задаче (4) – (5). Однако в (4) от второго легко избавиться, исключив из функции цели. Оказывается, что всегда при переходе к стохастической задаче можно избавиться от тех ограничений детерминированной задачи, коэффициенты которых являются случайными величинами. При этом появляется добавка в функции цели, которая учитывает убытки, появляющиеся при нехватке или излишке соответствующих ресурсов. Все величины получаются путем усреднения спроса с помощью соответствующих функций . В данном случае, даже не решая задачи, легко представить, что минимум полных затрат получится при .

В связи с тем, что здесь спрос считается случайной величиной, целевая функция становится нелинейной, а задача – стохастической; здесь целевая функция выпуклая и сепарабельная, так что задача решается методом линейной аппроксимации
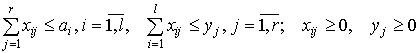
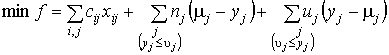