УДК:528

Математическая обработка инженерно-геодезических сетей в стереографической проекции Гаусса для Республики Кыргызстан

Динара Амалбековна Абжапарова, Бейшенбек Сыдыкбекович Ордобаев

Аннотация

В данной статье рассматривается математическая обработка инженерно – геодезических сетей в стереографической проекции Гаусса. Анализируются и классический метод – цилиндрическая проекция и новый - стереографические методы построения геодезической сети.

Mathematical processing of engineering and geodetic networks in a stereographic projection of Gauss.

Annotation

This article discusses the mathematical treatment of engineering - geodetic networks in the stereographic projection of the Gauss. Analyzed and compiled the classic method - cylindrical projection and the new - stereographic methods for constructing geodetic network.

Выбор и разработка геодезических проекции и системы координат для инженерно - геодезических работ в настоящее время является важной и актуальной проблемой инженерной геодезии, и представляет практический интерес. В своих исследованиях И.Ф.Куштин, В.И. Куштин (Россия)[3] в В.Н.Зенин (Кыргызская Республика) [4] внесли большой вклад в решении этих проблем. Однако в выше указанных работах слабо решены вопросы выбора и разработки геодезической проекции для создания городских геодезических сетей.

Целью настоящей работы является выбор и разработка специальной городской геодезической проекции и сети для инженерно - геодезических работ в Кыргызской Республике.

Для научного обоснования и сравнительной оценки достоинства стереографической проекции Гаусса, дадим математическую обработку одной и той же городской геодезической сети (рис. 1) в выше указанной системе, а также широко распространенной цилиндрической проекции [1,2].

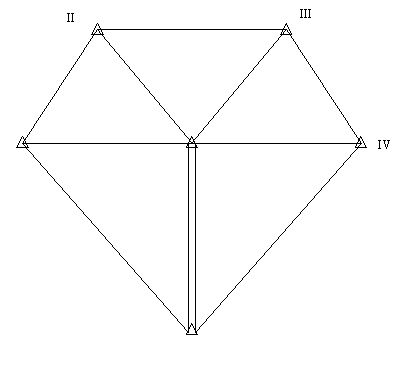
Рис. 1

Сеть, представленная на рис. 1, является центральной системой из пяти треугольников.

Сторона AB сети измерена электронным тахеометром TC802 швейцарской фирмы “Лейка” с относительной точностью 1:200000 и одновременно является стороной государственной триангуляции 3-го класса.

Исходными данными сети триангуляции являются:

а) координаты пункта А

длина стороны AB

и её направление в проекции Гаусса - Крюгера

б) измеренные углы сети на элипсоиденой поверхности табл. 1

Таблица 1

Название пункта	Измеренные углы
I B A	60°57′57,7" 69°27′44,8" 49°34′17,6"
II B I	56°33′40,7" 73°48′18,9" 49°41′04,5"
IV B III	56°33′40,7" 69°34′30,2" 53°35′04,3"
A B IV	37°58′23,8" 94°28′47,0" 47°32′51,3"
А В IV	58°38′43,9" 52°43′39,1" 68°37′38,5"

Получим исходные данные в оптимальной стереографической проекции Гаусса по соответсвующим элементам в системе координат Гаусса – Крюгера. Эти задачи легко решаются по схеме рис. 1.

1) Примим за начало координат городской системы точку с координатами:

В₀ = 55⁰ 00 ′ x₀ = 6097337,19 м

L₀ = 27⁰ 00′ R₀ = 6395543 м

Тогда

X_г.к = X-X_А = 10226,62 м

Y_г.к = Y_A= +71684,52 м

Вычислим с помощью табл. 2 координаты исходного пункта в городской системе.

Таблица 2

Элементы формул	Пункт А (м)
xGк - I + II XG	10226,62 - 0,31 + 0,00 10226,31
yGк + I - II yG	71684,32 + 0,04 - 0,75 73683,81

Получим масштаб изображения в пункте А по формуле и результат значений запишем в таблицу (табл. 3).

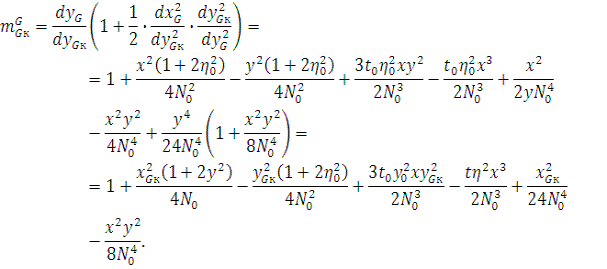(1)

Таблица 3

Элементы формул	Значения
I + +	1,0000000 0,0000006 0,0000315
	1,0000321

Найдём длину стороны в стереографической проекции по формулам (табл. 4).

Таблица 4

Элементы формулы	Значения (м)
+ -	6013,21 + 0,01 - 0,18
	6013,04

Определим дирекционный угол исходного направления в городской системе координат по формуле.

(2) Результаты полученных значений запишем в таблицу (табл. 5).

Таблица 5

Элементы формулы	Значения
	47′ 28,01” + 1,85 - 0,05 + 0,40 + 0,02
	47′ 30,30”

Дальнейшую математическую обработку геодезической сети выполним по новым исходным данным, соответствующим стереографической проекции Гаусса в городской системе координат [3,4].

Используя новые координаты пункта А, дирекционный угол , измеренные углы и длины сторон треугольников, полученные в таблице 1 вычислим приближённые координаты всех пунктов сети и определим поправки в направлениях за кривизну изображения геодезических линий на плоскости в стереографической проекции Гаусса по приближённым значениям координат [2,3], вычислим поправки в углы, найдем плоские углы и выполним уравнивание сети двух групповым методом [6,7].

Затем выполним окончательное решение треугольников, используя значения сторон треугольников сети и дирекционные углы, вычислим окончательные координаты в стереографической проекции Гаусса, а также выполним контроль полученных результатов.

Таблица 6

Пункты
A B I II III IV	10226,31 14885,53 10363,48 16043,51 19455,03 15071,80	71683,81 67882,72 65245,08 63241,47 67368,91 73393,68

Как видно из таблицы 6 переход с эллипсоида на плоскость в стереографической проекции сопровождается гораздо меньшими искажениями, чем проекции Гаусса-Крюгера, в среднем в 2 раза.

Определим границы области применения проекции для сетей сгущения съемочного обоснования.

Согласно математической обработке инженерно-геодезических сетей имеем [8].

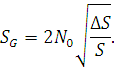(3)

Для исходной стороны триангуляции 4 класса при получим

Площадь обхвата в данном случае будет

Отсюда, если принять за начало координат в стереографической проекции какую-либо точку, расположенную на ближайшем осевом меридиане зоны под широтой изображаемого города, то на площади 5000 км², т.е. 70х70 км², при относительной точности 1:100000, линейными искажениями городской триангуляции можно будет пренебречь.

Для городской полигонометрии всех разрядов линейными искажениями 1:20000 и ниже можно пренебречь на площади [10,11].

P = 3,14·80² = 20 000 км² = 140 х 140 км².

Для съемочного обоснования, развиваемого с относительной ошибкой 1:2000, можно пренебречь на площади в 1 лист масштаба 1:1000000.

В таблице 7 приведены значения величины линейных искажений в стереографической проекции Гаусса для инженерно-геодезических работ в зависимости от их точности.

В расчетах длина стороны геометрического построения равна 1 км.

Поправки вычислены по формуле

∆S=1км∙S²_G /4N²₀ (4)

Таблица 7

Расстояние от начала координат, км	Ошибка в расстоянии на 1 км, м	Поправка на 1 км, м	Относительная ошибка
0 10 20 30 40 50 100 120 150 200 250 285	0 0 +0,002 +0,006 +0,010 +0,016 +0,064 +0,090 +0,140 +0,260 +0,400 +0,500	0 0 -0,002 -0,006 -0,010 -0,016 -0,064 -0,090 -0,140 -0,260 -0,400 -0,500	- - 1:500000 1:160000 1:100000 1:60000 1:16000 1:11000 1:7000 1:4000 1:2500 1:2000

Полученные результаты дают возможность сделать следующих выводов:

1. При обработке высокоточных инженерно-геодезических сетей порядка 1:100000 и выше, следует учитывать результаты редукции.

2. При обработке сетей сгущения редуцирование не осуществляется по всей ширине 3⁰ зон .

3. При обработке съемочного обоснования и результатов численных съемок редукции расстояний не учитываются по всей ширине 6⁰ зон .

4. При обработке угловых измерений сетей сгущения и съемочного обоснования редукциями направлений и углов можно пренебречь во всех случаях практики.

5. В случае использования секущей стереографической проекции Гаусса, границы использования систем координат увеличиваются в раз. Поэтому данная проекция также целесообразна для применения её в инженерно-геодезических работах, т.к. приводит к упрощению расчетов при математической обработке обоснования и исходных данных по выносу проектов в натуру.

Литература

1. Христов В.К. Координаты Гаусса-Крюгера на эллипсоде вращения. - М.: Геодезиста, 1957. – 203 с.

2. Болшаков В.Д. Практикум по теории математической обработки годезических измерений. – М .: Недра, 1983. – 223 с.

3. Куштин И.Ф., Куштин В.И. Геодезия: учебно-практической пособие- Ростов н/Д: Феникс, 2009. – 909 c.

4. Зенин В.Н. разработка специальной геодезической проекции для инженерных и городских геодезических работ// Автореферат диссертации на соискание ученной степени кандидата технических наук. – М.: 1970. – 12 с.

5. Голубев В.В. Теория математической обработки геодезических измерений. – М.: Недра, 2009. – 2 46 с.

6. Бойко Е.Г. Высшая геодезия // Часть II. Сфероидическая геодезия – Картгеоцентр. – М.: Геодезиздат, 2003. – 144 с.

7. Огородова Л.В. Высшая геодезия // Часть III. Теоретическая геодезия. – М.: Геодезкартиздат, 2006. – 245 с.

8. Яковлев Н.В. Высшая геодезия. – М.: Недра, 1989. – 445 с.

9. Пеллинен Л.П. Высшая геодезия. – М.: Недра, 1978. – 264 с.

10. Бессель Ф.В. Высшая геодезия и способ наименьших квадратов. – М.: Геодезлитиздат, 1961. – 282 с.

11. Карабцова З.М. Геодезия. – М.: Издательство Дальневосточного университета, 2002. – 153 с.